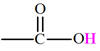|
TP Chimie N° 04 |
Simulation de spectres RMN avec le logiciel HNMR Spectrum. Correction |
|
|
|
I. Simulation
de spectres RMN de quelques molécules avec le logiciel
1HMNR.
► Tableau de déplacement chimique
δ (ppm) de quelques protons :
|
Groupe méthyle CH3
– |
Groupe méthylène – CH2
– |
||
|
Proton |
δ ppm |
Proton |
δ ppm |
|
CH3
– C |
0,9 |
C – CH2
– C |
1,3 |
|
CH3
– C – O |
1,4 |
C – CH2
– Ccycle |
1,5 |
|
CH3
– C = C |
1,6 |
C – CH2
– C – O |
1,9 |
|
|
2,3 |
C – CH2
– C = C |
2,3 |
|
|
2,2 |
|
2,7 |
|
|
2,6 |
|
2,4 |
|
|
2,0 |
|
2,2 |
|
|
2,4 |
C – CH2
– O – R |
3,4 |
|
|
2,0 |
C – CH2
– O – H |
3,6 |
|
CH3
– O – R |
3,3 |
|
4,3 |
|
CH3
– OH |
3,4 |
|
4,1 |
|
|
3,8 |
C – CH2
– N |
2,5 |
|
|
3,7 |
|
2,4 |
|
|
2,3 |
C – CH2
– Cl |
3,4 |
|
|
2,0 |
C – CH2
– C – Cl |
1,7 |
|
CH3
– Cl |
3,0 |
C – CH2
– Br |
3,3 |
|
|
1,5 |
C – CH2
– C – Br |
1,7 |
|
CH3
– Br |
2,7 |
C – CH2
– I |
3,1 |
|
|
1,7 |
C – CH2
– C – I |
1,8 |
|
CH3
– I |
2,2 |
|
2,3 |
|
|
1,9 |
C – CH2
– C – C = C
|
1,5 |
|
|
2,0 |
|
3,8 |
|
Groupe méthyne
|
|
|
Proton |
δ ppm |
|
|
1,5 |
|
|
2,0 |
|
|
3,0 |
|
|
2,7 |
|
|
3,7 |
|
|
3,9 |
|
|
4,8 |
|
|
2,8 |
|
|
4,0 |
|
|
1,6 |
|
|
3,6 |
|
|
1,7 |
|
|
4,2 |
|
|
1,9 |
|
|
2,7 |
► Autres groupes :
|
Autres groupes |
Autres groupes
(suite) |
||
|
Proton |
δ (ppm) |
Proton |
δ (ppm) |
|
|
5,3 |
|
8,0 |
|
|
5,1 |
|
8,0 |
|
C6H6 |
7,2 |
|
8,5 - 13 |
|
|
7,0 – 9,0 |
|
11 - 17 |
|
|
3,1 |
R – OH |
0,5 – 5,5 |
|
|
9,9 |
|
4,5 – 7,1 |
|
|
9,9 |
|
0,6 - 5 |
2)- Construire les spectres
RMN
à l’aide du logiciel HNMR Spectrum :
-
Cliquer sur le raccourci :

-
Cliquer sur ACD/Labs
-
Dans le menu déroulant, cliquer
sur ![]()
-
Il apparaît la fenêtre suivante :
-
Sélectionner : ![]()
-
Dans le menu : Tools,
sélectionner Simulation
-
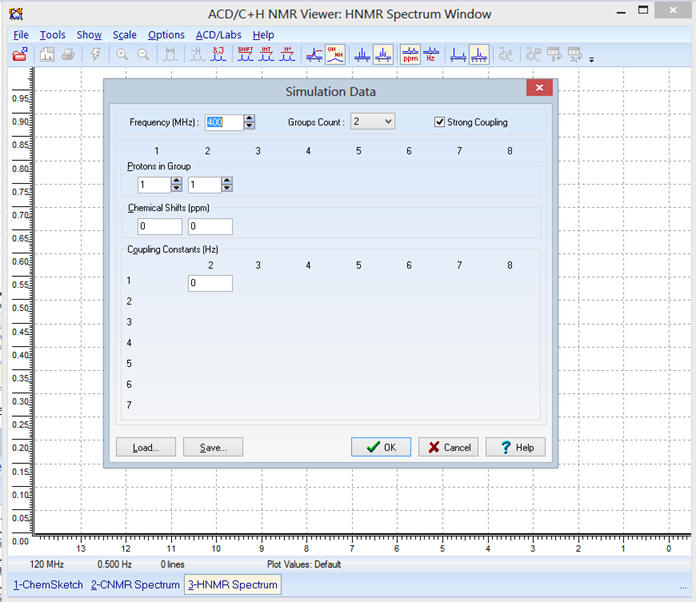
Il apparaît la fenêtre suivante :
- Pour pouvoir construire le spectre RMN de la molécule:
- Il faut connaître les
différents déplacements chimiques des groupes de protons
équivalents qui constituent la molécule.
-
Le but de l’exercice et de
remplir le tableau « SIMULATION DATA » afin d’afficher le
spectre de la molécule :
-
Pour ce faire, il faut :
-
Indiquer la valeur de la
fréquence : f
-
Cette fréquence
f
représente la valeur de la fréquence de résonance des protons de
l’échantillon de référence.
-
Elle est liée à la valeur du
champ magnétique imposé par l’appareil de
RMN.
-
Ainsi un appareil de
RMN à
9,4 T est appelé spectromètre de 400 MHz.
-
Il y a proportionnalité entre la
valeur de l’intensité du champ magnétique appliqué et la
fréquence f de résonance des protons de l’échantillon de
référence.
► Tableau de correspondance :
|
Valeur de
l’intensité du champ
magnétique
de l’appareil
RMN |
1,41 T |
2,11 T |
2,4 T |
4,7 T |
7,1 T |
9,4 T |
|
Fréquence de résonance des
protons de l’échantillon de référence |
60 MHz |
90 MHz |
100 MHz |
200 MHz |
300 MHz |
400 MHz |
-
Dans un premier temps, on prendra
90 MHz, puis on pourra changer cette valeur pour voir
l’influence sur l’affichage du spectre.
-
Groups Count : Indiquer le
nombre de groupes équivalents de la molécule à l’aide du petit
ascenseur.
-
Strong Coupling : Décocher
dans un premier temps cette option.
-
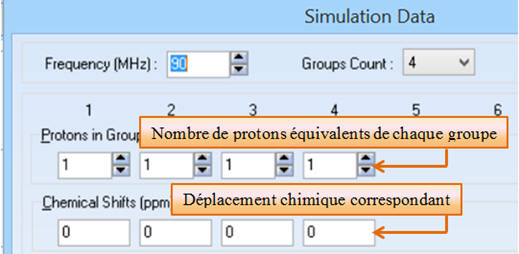
Protons in
Group et
Chemical shifts (ppm) :
-
Il faut indiquer le nombre de
protons équivalents de chaque groupe et le déplacement chimique
correspondant au-dessous.
-
On commence par le groupe dont le
déplacement chimique est le plus important et ainsi de suite.
-
Coupling Constants
(Hz):
-
Rentrer les valeurs des
constantes de couplages.
-
Constante de couplage
J
entre les deux protons : Distance entre 2 pics d’un signal.
- Les constantes de couplage J sont exprimées en hertz.
- La valeur de la constante de couplage est indépendante de l’intensité du champ magnétique appliqué et
- ne dépend que du nombre et de la nature des liaisons
séparant les deux protons et de la disposition spatiale des
protons.
► On utilise les règles suivantes :
-
Les effets du couplage
disparaissent rapidement avec la distance.
-
Les atomes d'hydrogène portés par
des atomes adjacents de carbone présentent
un effet de couplage notable (4 Hz
≤ J
≤ 10 Hz).
- Les atomes d'hydrogène éloignés (deux hydrogènes séparés par plus de deux carbones) les uns des autres ne subissent presque pas
- d’effets réciproques (0 Hz
≤ J
≤ 1 Hz).
-
Le pic du proton hydroxyle
apparaît généralement sous la forme d'un singulet.
- Atome d’hydrogène du groupe hydroxyle :
- Du fait de la mobilité de l'atome d'hydrogène du groupe hydroxyle,
- le couplage avec les autres protons (protons
portés par le carbone voisin) disparaît (J
≈ 0 Hz).
II.
Réalisation des spectres :
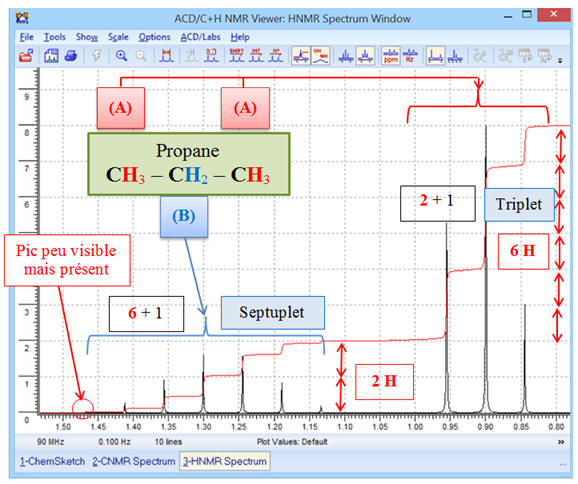
1)- Molécule de propane :
CH3
– CH2 –
CH3
a)- Collecte des différentes valeurs
et analyse de la molécule.
-
Nombre de groupes de protons
équivalents : 2
-
Analyse de la molécule :
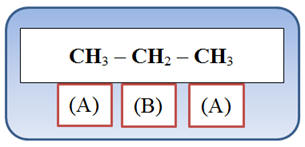
-
Compléter le tableau récapitulatif du type
suivant à l’aide du tableau de données et de l’analyse de la
molécule :
|
|
Groupe (A) |
Groupe (B) |
Groupe (C) |
Groupe (D) |
|
Atomes d’hydrogène |
6 |
2 |
|
|
|
Déplacement chimique (ppm) |
|
|
|
|
|
Nombre de pics du signal |
|
|
|
|
|
Nombre de
protons Équivalents
voisins |
|
|
|
|
► Remarque pour la constante de
couplage, on prendra J
≈ 5 Hz.
-
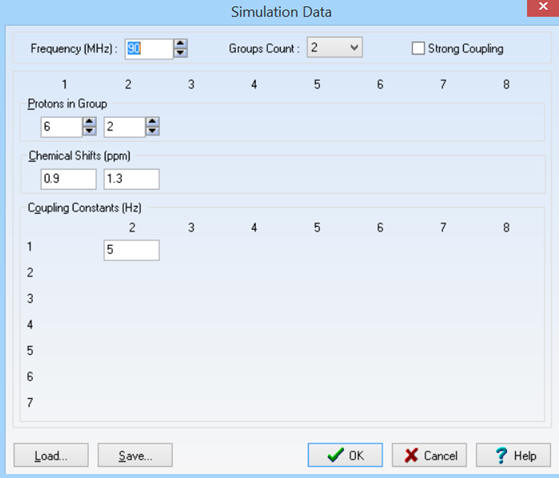
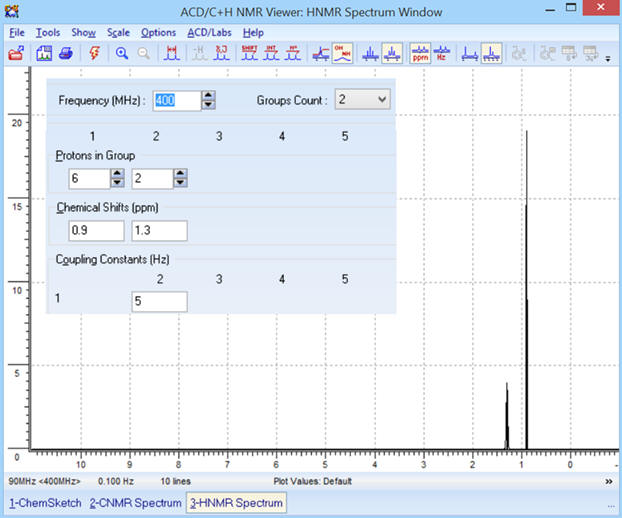
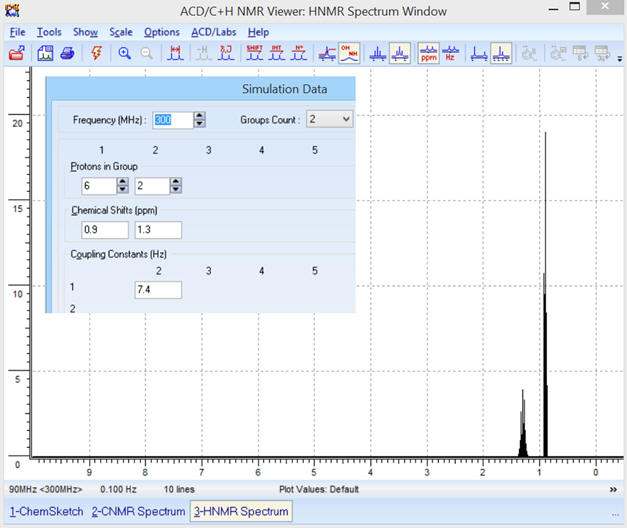
Les différents paramètres :
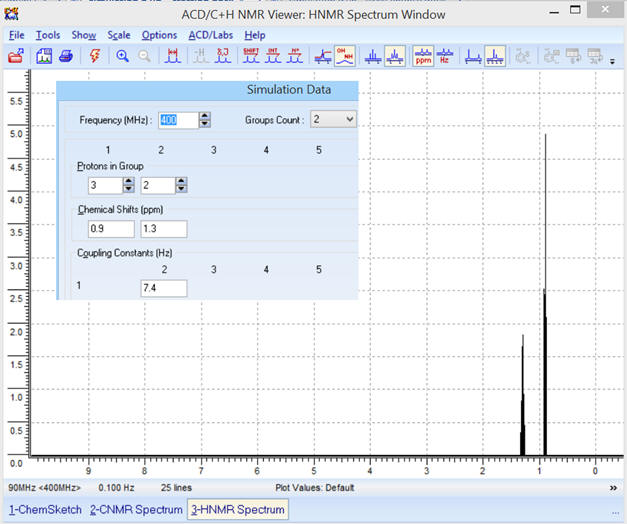
SIMULATION DATA.
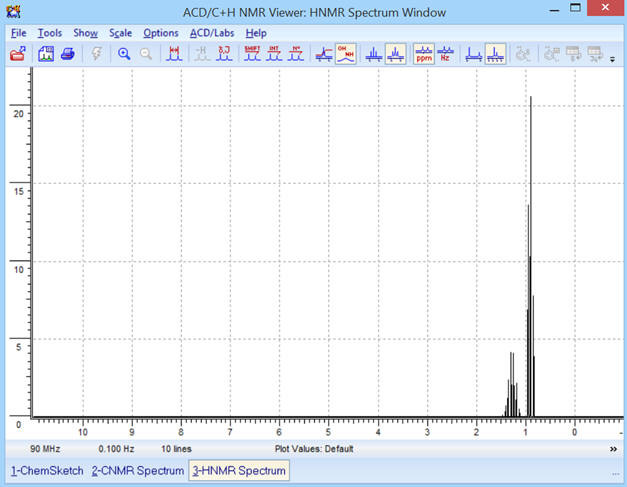
-
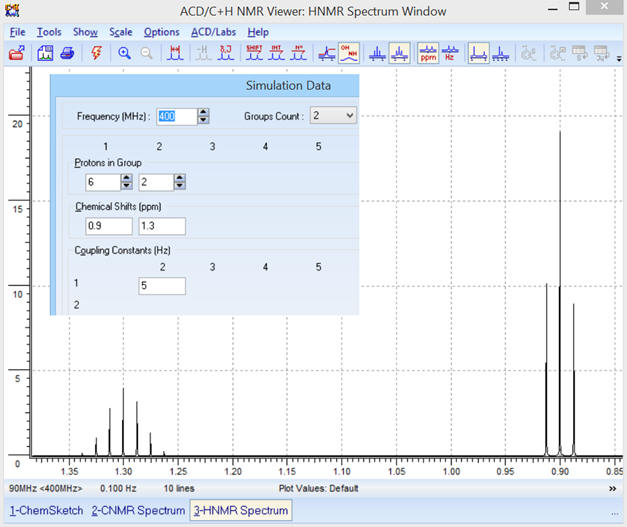
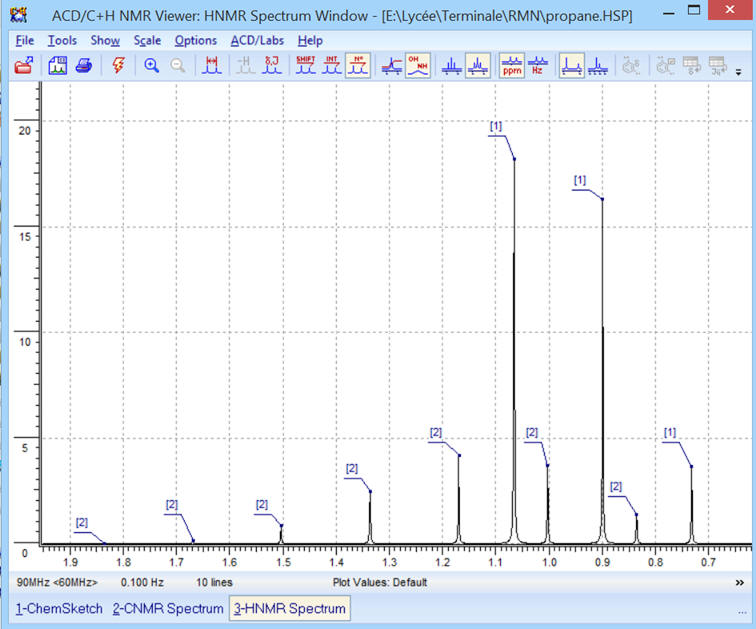
On obtient le spectre suivant :
- Remarque : Pour la fréquence f = 90 MHz, la valeur du couplage ne doit pas être trop grande car autrement,
- les deux signaux se superposent (on prend
J
= 5 Hz).
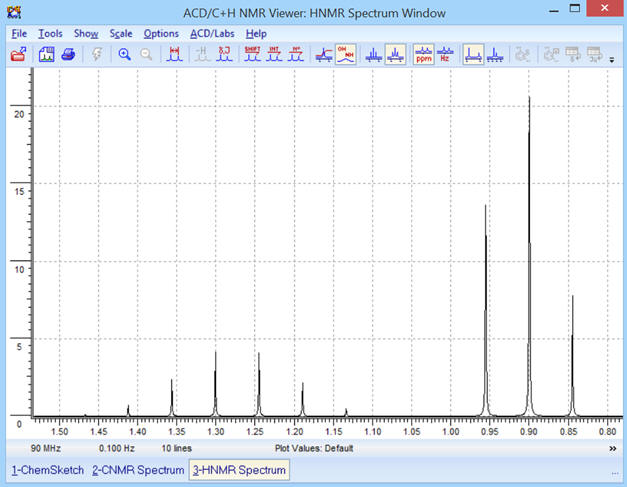
-
Optimisation et exploitation du spectre
obtenu :
-
Commentaires :
-
Le spectre obtenu est bien
conforme à la molécule :
-
On observe la présence de deux
signaux.
- Le signal du groupe (A) (deux groupes méthyle CH3 –) est constitué d’un triplet (2 + 1),
- Il possède deux
protons équivalents voisins (groupe (B) groupe méthylène
– CH2
–).
- Le signal du groupe (B) (groupe méthylène – CH2 –) est constitué d’un septuplet (6 + 1),
- Il possède 6
protons équivalents voisins (deux groupes méthyle CH3
–)
-
Ceci correspond bien à la
molécule de propane : CH3 –
CH2
– CH3
c)- Modification de la fréquence
f
et comparaison :
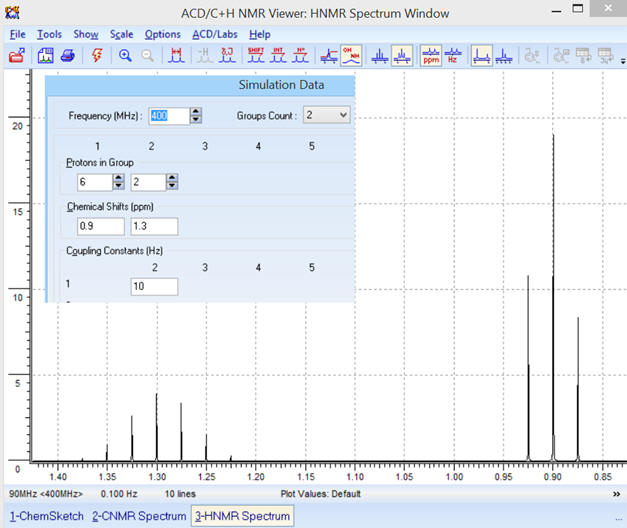
► f = 400 MHz
-
Les déplacements chimiques sont
inchangés et les signaux du spectre
RMN
sont plus resserrés.
-
Optimisation des échelles :
-
Constante de couplage :
J
= 10 Hz
-
Remarques :
-
Lorsque l’on augmente la valeur
de la constante de couplage l’écart entre les différents pics
augmente.
-
La constante de couplage
représente l’écart en Hz entre deux pics.
-
On peut réaliser une mesure :
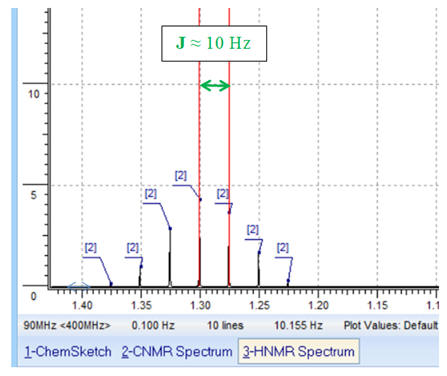
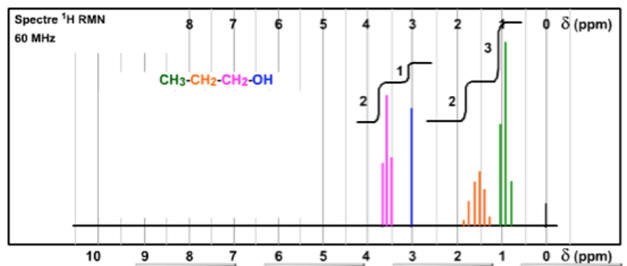
► f =
60 MHz.
-
Remarques : on prend
f =
60 MHz et J = 10 Hz
-
Spectre
RMN :
-
On remarque que les deux signaux
se superposent.
-
Le spectre est plus difficile à
exploiter.
- Lorsque la constante de couplage est élevée et que les signaux ont des déplacements chimiques proches :
- Il faut prendre une fréquence f élevée permet empêcher
l’enchevêtrement des signaux.
- La valeur de la constante de couplage est indépendante de l’intensité du champ magnétique appliqué et
- ne dépend que du nombre et de la nature des liaisons
séparant les deux protons et de la disposition spatiale des
protons.
-
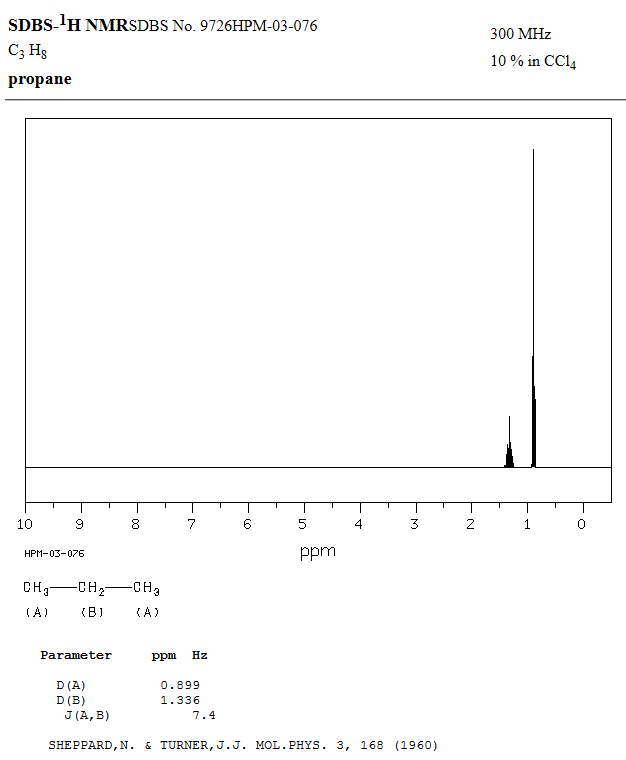
Comparaison du spectre obtenu
avec HNMR Spectrum à
celui donné par le site :
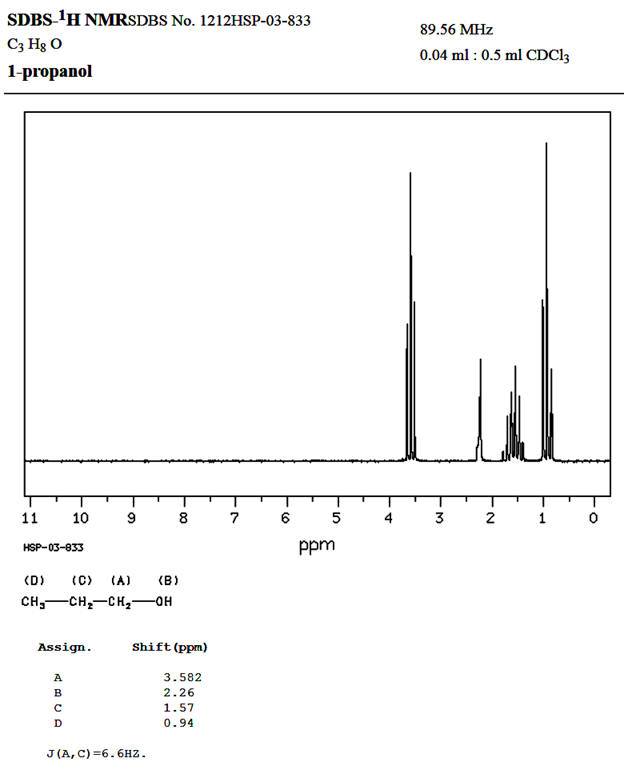
SDBS –
1HNMR.
-
URL du site :
https://sdbs.db.aist.go.jp/sdbs/cgi-bin/direct_frame_top.cgi
-
Pour pouvoir comparer les deux
spectres RMN, on choisit comme fréquence f
= 300 MHz et
comme valeur du couplage :
J = 7,4 Hz
-
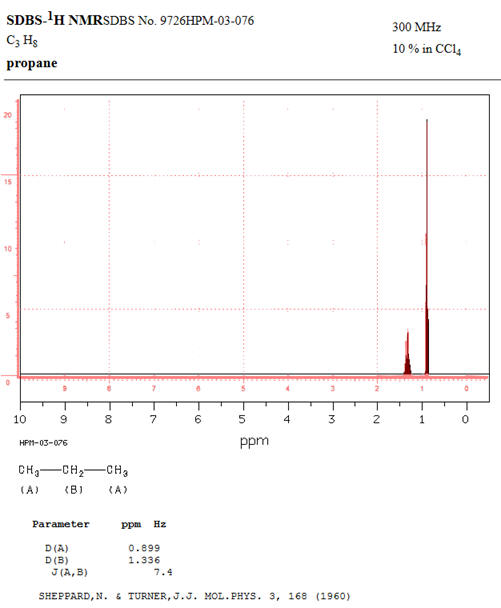
En respectant les mêmes valeurs
et les mêmes échelles, on remarque que les deux spectres sont
analogues (2 signaux).
-
Les deux spectres sont
superposables :
III. Recommencer l’étude pour les
molécules suivantes :
|
-
Indiquer le nombre de groupes de protons
équivalents :
- Réaliser l’analyse de la molécule :
-
Compléter le tableau du type suivant à l’aide du
tableau de données :
- Obtenir le spectre à l’aide du logiciel 1 HNMR
Spectrum.
- Optimiser l’affichage.
-
Commenter le spectre obtenu.
|
1)- Molécule de formule brute
C4H10.
(Attention aux isomères)
a)-
Le n butane :
CH3 –
CH2 –
CH2
– CH3
-
Nombre de groupes de protons
équivalents : 2
-
Analyse de la molécule :
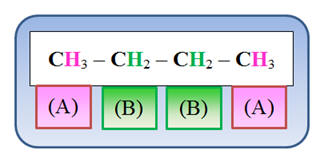
-
Tableau récapitulatif :
|
|
Groupe (A) |
Groupe (B) |
Groupe (C) |
Groupe (D) |
|
Atomes
d’hydrogène |
6 |
4 |
|
|
|
Déplacement
chimique (ppm) |
0,9 |
1,3 |
|
|
|
Nombre de pics
du signal |
3 |
4 |
|
|
|
Nombre de protons
Équivalents voisins |
2 |
3 |
|
|
-
Les 6 protons portés par les
groupes CH3 – aux deux extrémités de la
molécule sont équivalents.
-
De même les 4 protons portés par
les groupes – CH2 – au centre de la molécule
sont équivalents.
-
Le spectre
RMN de la
molécule de n butane présente deux signaux.
-
Le rapport entre les nombres de
protons équivalents des deux groupes est de 3 pour 2 (6 pour 4).
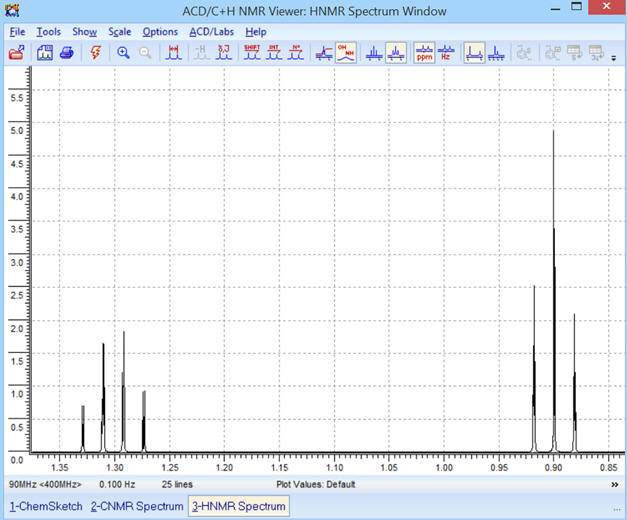
► Obtention du spectre :
-
Constante de couplage : on prend
J23 =
JAB
≈ 7,4 Hz
-
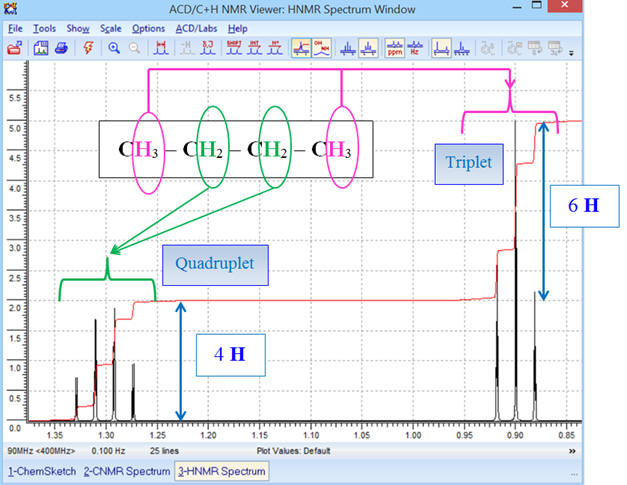
Optimisation de l’affichage :
-
Avec la courbe d’intégration :
-
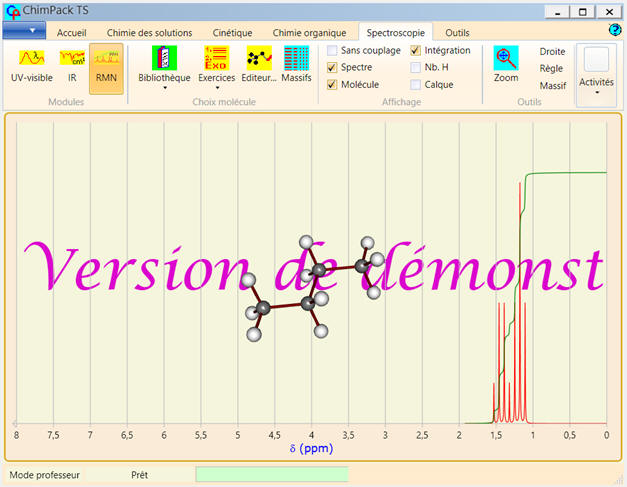
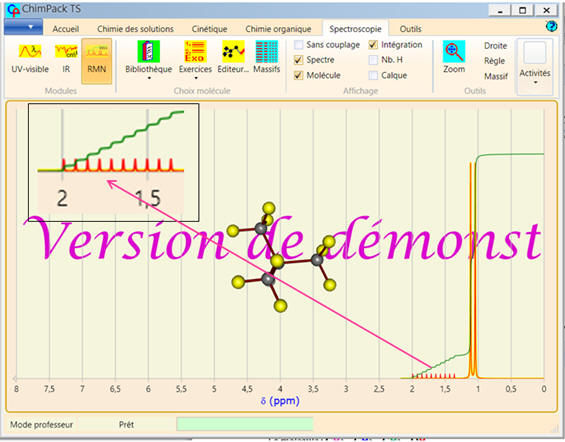
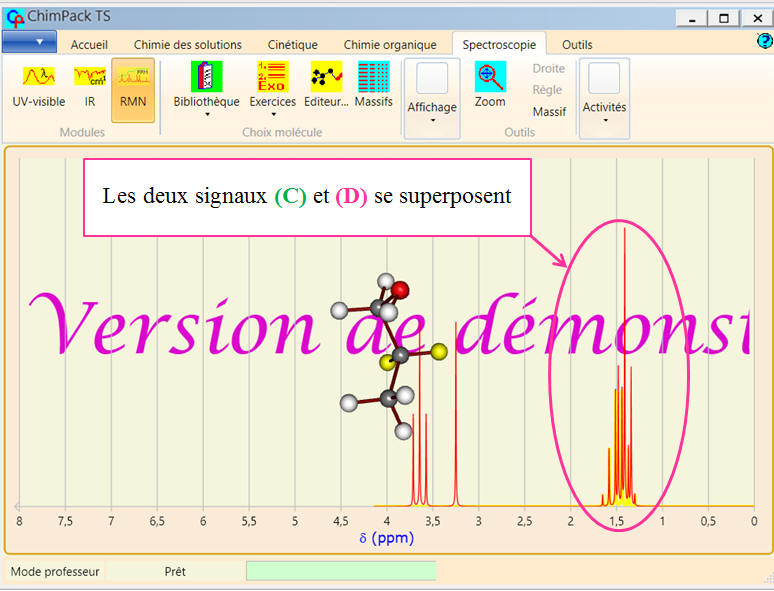
Avec le logiciel de simulation
RMN de ChimPack TS :
-
Dommage que l’on ne puisse pas
changer la fréquence de résonnance.
-
En cliquant sur un atome de la
molécule, les atomes équivalents sont mis en évidence ainsi que
le signal correspondant sur le spectre.
-
Le site
SDBS –
1HNMR
ne donne pas le spectre RMN du butane.
-
URL du site :
https://sdbs.db.aist.go.jp/sdbs/cgi-bin/direct_frame_top.cgi
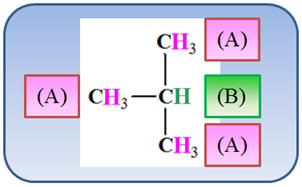
a)- Le 2-méthylpropane :
-
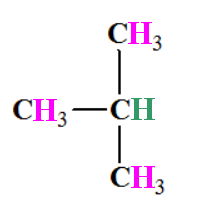
-
Nombre de groupes de protons
équivalents : 2
-
Analyse de la molécule :
|
|
Groupe (A) |
Groupe (B) |
Groupe (C) |
Groupe (D) |
|
Atomes d’hydrogène |
9 |
1 |
|
|
|
Déplacement chimique (ppm) |
0,9 |
1,5 |
|
|
|
Nombre de pics du signal |
2 |
10 |
|
|
|
Nombre de protons Équivalents voisins |
1 |
9 |
|
|
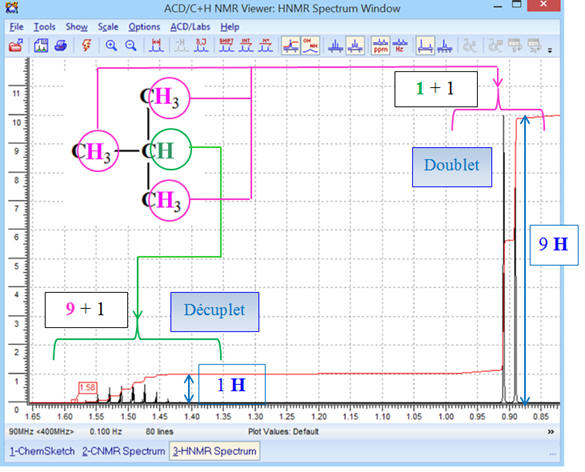
-
Les 9 protons portés par les
groupes CH3 – aux extrémités de la molécule
sont équivalents.
-
Le proton isolé sur le carbone
central n’a pas d’équivalent

-
Le spectre
RMN de la
molécule de 2-méthylbutane présente deux signaux.
-
Le rapport entre les nombres de
protons équivalents des deux groupes est de 9 pour 1.
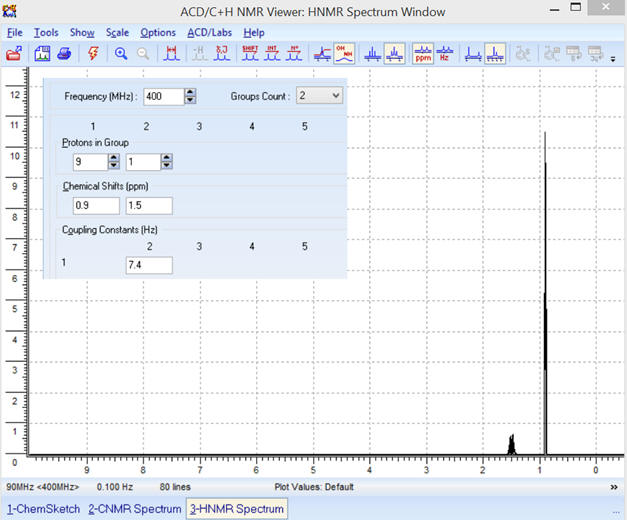
► Obtention du spectre :
-
Comme fréquence on choisit :
f
= 400 MHz
-
Constante de couplage : on prend
J23 =
JAB
≈
7,4 Hz
-
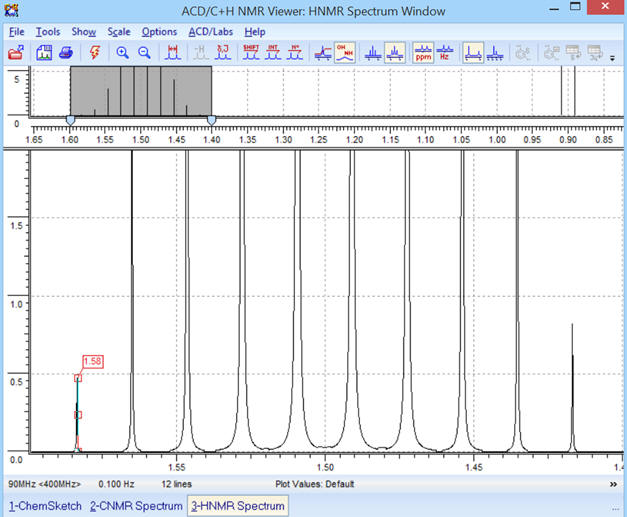
Avec la courbe d’intégration et optimisation:
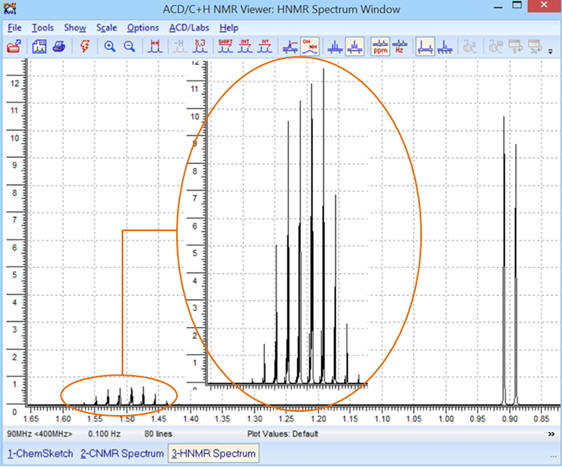
-
Le premier pic du signal (B) n’est pas bien
visible.
-
On peut réaliser un
ZOOM sur la partie concernée :
-
ZOOM sur la partie entourée :
-
Avec le logiciel de simulation
RMN de ChimPack TS :
-
Le site
SDBS –
1HNMR
ne donne pas le spectre RMN du 2-méthylpropane.
-
URL du site :
https://sdbs.db.aist.go.jp/sdbs/cgi-bin/direct_frame_top.cgi
-
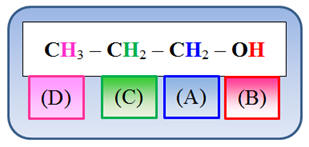
La molécule : CH3
– CH2 –
CH2
– OH
-
Nombre de groupes de protons équivalents : 4
-
Analyse de la molécule :
-
Tableau récapitulatif : le remplissage se fait à l’aide
du tableau de données.
|
(A) |
C – CH2
– O – H |
3,6 |
|
(B) |
R – OH |
0,5 – 5,5 on prend
2,26 |
|
(C) |
C – CH2
– C |
1,3 |
|
(D) |
CH3
– C |
0,9 |
|
|
Groupe (A) |
Groupe (B) |
Groupe (C) |
Groupe (D) |
|
Atomes d’hydrogène |
2 |
1 |
2 |
3 |
|
Déplacement chimique (ppm) |
3,6 |
2,26 |
1,3 |
0,9 |
|
Nombre de pics du
signal |
3 |
1 |
6 |
3 |
|
Nombre de protons Équivalents
voisins |
2 |
0 |
5 |
2 |
-
Spectre à l’aide du logiciel
HNMR Spectrum :
-
Pour les couplages :
-
JAB =
J12 ≈ 0 ;
JAC
= J13 ≈ 7 Hz ;
JAD =
J14
≈ 0 Hz ;
-
JBC =
J23 ≈ 0 ;
JBD
= J24 ≈ 0 Hz ;
-
JCD =
J34 ≈ 7 Hz ;
-
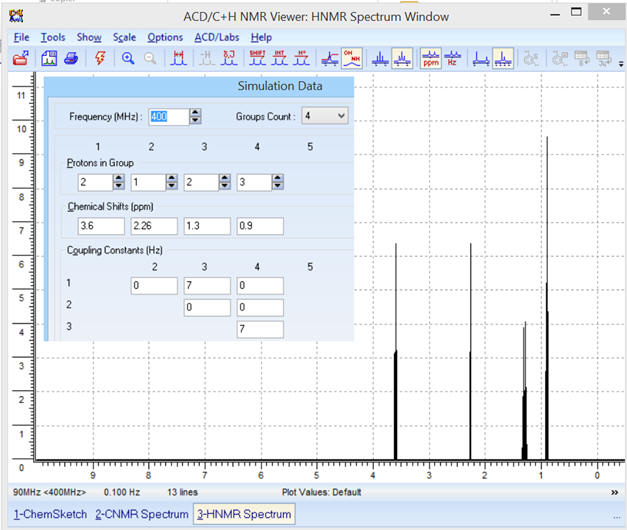
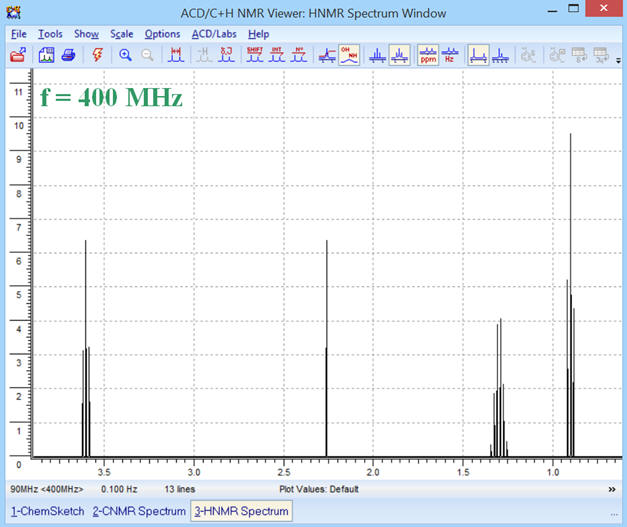
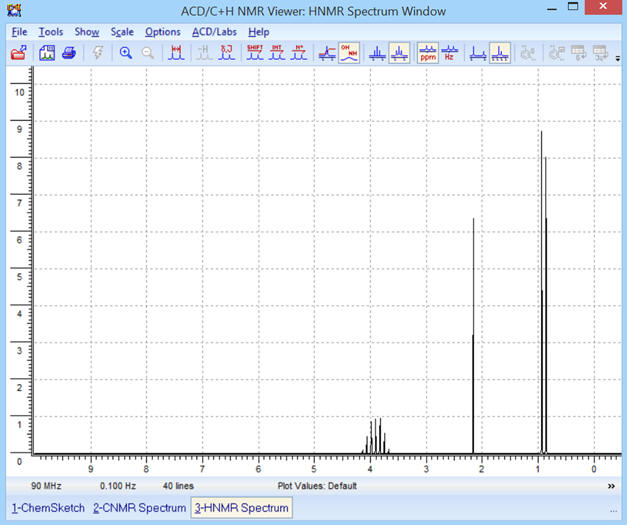
Pour une fréquence
f = 400 MHz, on obtient le
spectre RMN suivant :
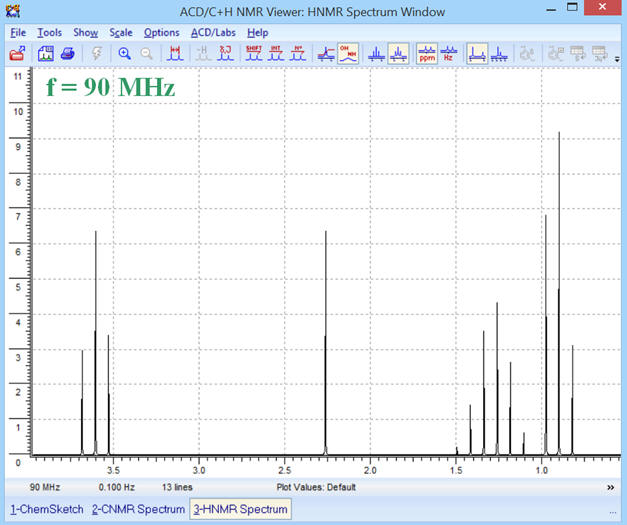
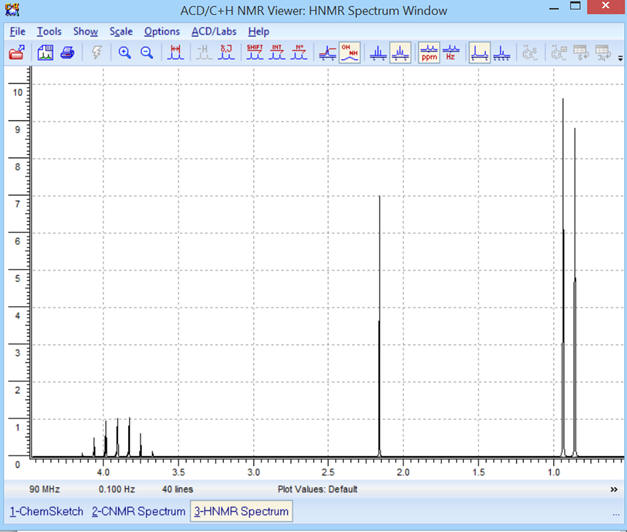
-
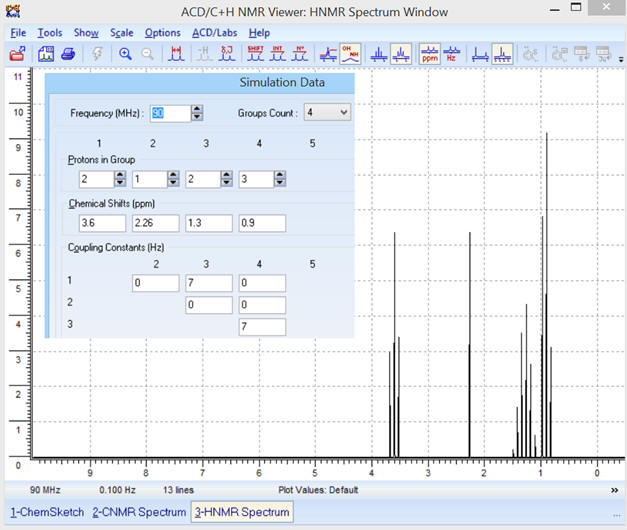
Pour une fréquence
f = 90 MHz, on obtient le
spectre RMN suivant :
-
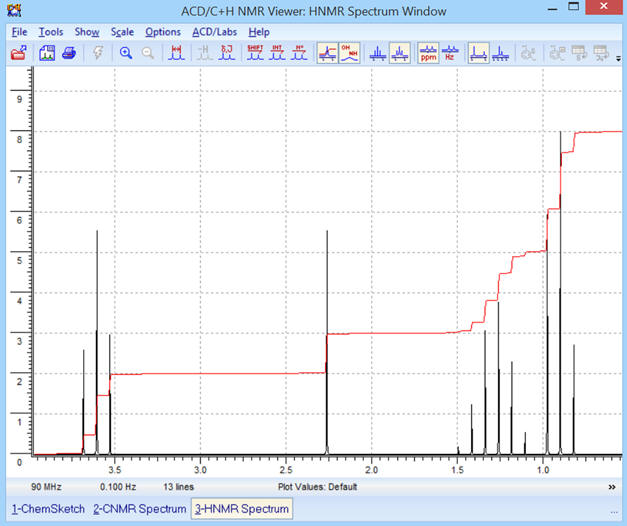
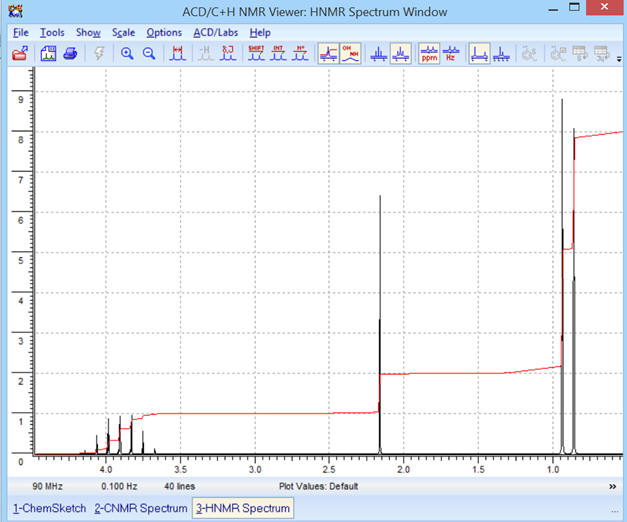
Optimisation de l’affichage :
-
Avec la courbe d’intégration :
-
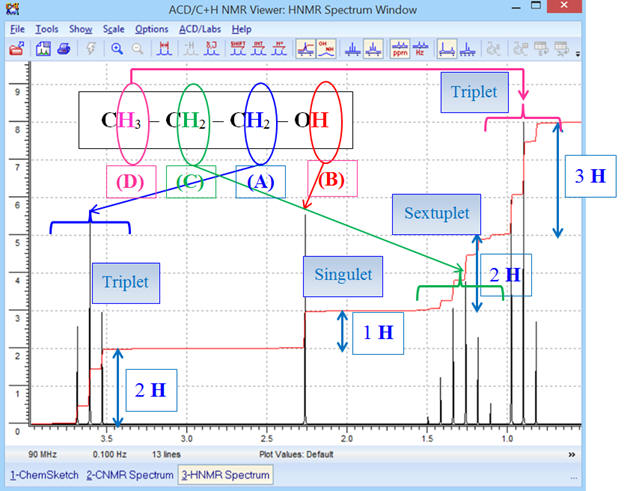
Commentaires :
-
Le déplacement chimique d’un groupe de protons
équivalents est d’autant plus grand que l’atome de carbone, qui
les porte, est proche de l’atome d’oxygène.
- Le signal du groupe (A) (groupe méthylène – CH2 –) est constitué d’un triplet (2 + 1),
- Il possède deux
protons équivalents voisins (groupe (C) groupe méthylène
– CH2
–).
- Le signal du groupe (B) (groupe hydroxyle – OH) est constitué d’un singulet (0 + 1).
- De façon générale,
il n’existe pas de couplage entre le proton du groupe hydroxyle
et les protons du groupe (A), groupe méthylène –
CH2
–.
-
Ceci est lié à la mobilité du proton hydroxyle, à son
caractère acide.
-
En milieu acide, le proton du groupe hydroxyle s’échange
avec le proton de l’acide.
- Cet échange est suffisamment rapide, devant le temps d’acquisition du spectre RMN,
- pour que les protons du groupe méthylène – CH2 – ne voient pas les deux états de spin (+ ½ et – ½) du proton du groupe hydroxyle.
- Tout se passe comme s’il n’y avait pas de
couplage.
- Le signal du groupe (C) (groupe méthylène – CH2 –) est constitué d’un sextuplet (5 + 1).
- Il possède 5
protons équivalents voisins : groupe méthylène (A) –
CH2
– et groupe méthyle (D)
CH3
–.
- Le signal du groupe (D) (groupe méthyle CH3 –) est constitué d’un triplet (2 + 1).
- Il possède deux
protons équivalents voisins (groupe (C) groupe méthylène
– CH2
–).
-
Spectre donné par le site
SDBS-1HNMR
-
Comparaisons :
-
La constante de couplage
JCD n’est pas
donnée.
|
|
|
Groupe (A) |
Groupe (B) |
Groupe (C) |
Groupe (D) |
|
Spectre obtenu |
Déplacement
chimique (ppm) |
3,6 |
2,26 |
1,3 |
0,9 |
|
Nombre de
pics du signal |
3 |
1 |
6 |
3 |
|
|
Site
SDBS-1HNMR |
Déplacement
chimique (ppm) |
3,582 |
2,26 |
1,57 |
0,94 |
|
|
3 |
1 |
6 |
3 |
-
Il y a une différence notable au niveau de la valeur du
déplacement chimique du groupe (C).
-
Cela provient du fait que l’on a utilisé la valeur donnée
dans le tableau de données :
|
C – CH2
– C |
1,3 ppm |
-
En réalité, le décalage est plus important car il y a la
présence de l’atome d’oxygène du groupe hydroxyle (groupe (B).
|
C – CH2
– C – O |
1,9 ppm |
-
On peut aussi choisir cette valeur donnée dans le tableau
de données.
-
Ce phénomène est moins visible pour le déplacement
chimique du groupe (D), car ce groupe est encore plus
éloigné de l’atome d’oxygène du groupe hydroxyle.
-
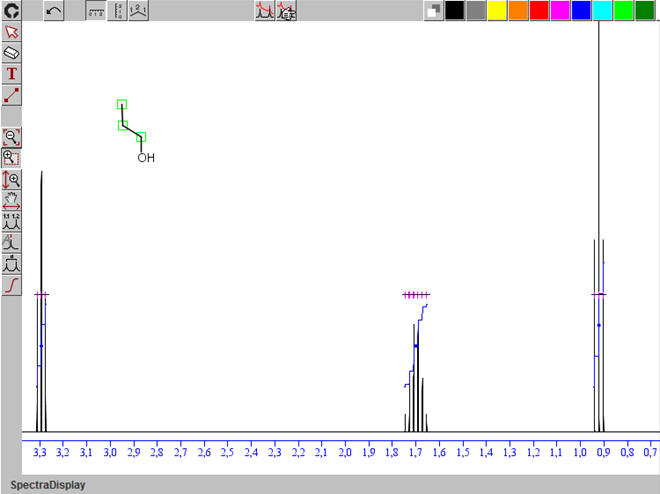
Autre spectre du propan-1-ol :
-
Avec le logiciel de simulation RMN de ChimPack TS :
-
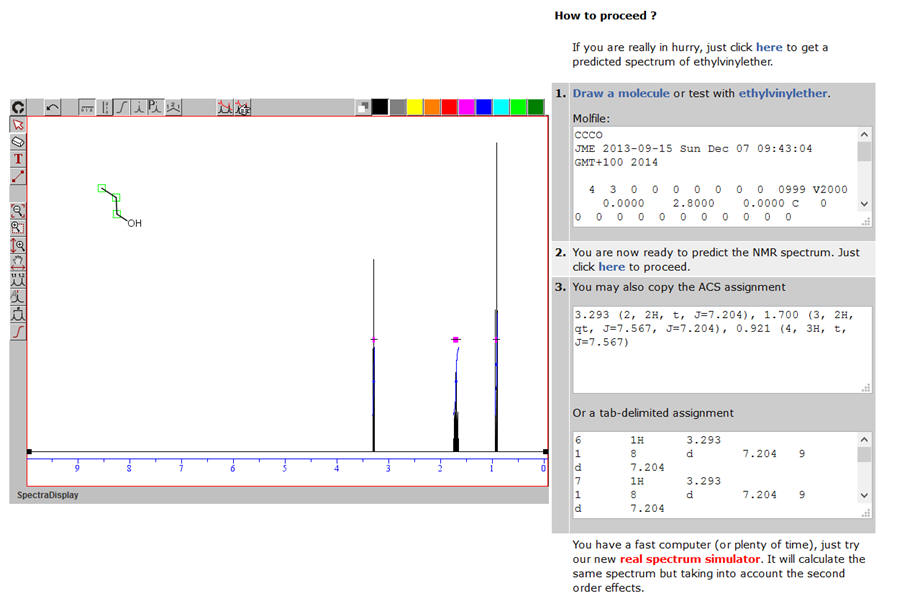
Avec le logiciel de simulation :https://www.nmrdb.org/predictor/
-
On clique sur « Draw a molecule »
-
On construit la molécule, puis on clique sur « Submit
Molecule »
-
On obtient le spectre suivant avec les valeurs
associées :
- On remarque que le spectre RMN ne comprend que 3 signaux.
- Il manque le signal relatif au proton du groupe
hydroxyle (singulet à 2,26 ppm).
-
On effectue un zoom :
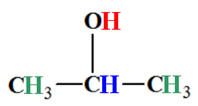
-
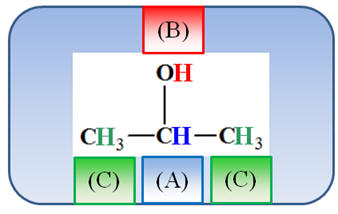
Nombre de groupes de protons équivalents : 3
-
Analyse de la molécule :
-
Tableau récapitulatif : le remplissage se fait à l’aide du
tableau de données.
|
(A) |
|
3,9 ppm |
|
(B) |
R – OH |
0,5 – 5,5 on prend
2,16 ppm |
|
(C) |
CH3
– C |
0,9 ppm |
|
|
Groupe (A) |
Groupe (B) |
Groupe (C) |
|
Atomes
d’hydrogène |
1 |
1 |
6 |
|
Déplacement
chimique (ppm) |
3,9 |
2,16 |
0,9 |
|
Nombre de
pics
du signal |
7 (6 + 1) |
1 |
2 (1 + 1) |
|
Nombre de protons
Équivalents voisins |
6 |
0 |
1 |
-
Constantes de couplages :
-
JAB =
J12 ≈ 0 ;
JAC
= J13 ≈ 7 Hz ;
-
JBC =
J23 ≈ 0 ;
-
Affichage du spectre avec le logiciel
HNMR Spectrum :
-
Optimisation :
-
Courbe d’intégration :
-
Commentaires :
-
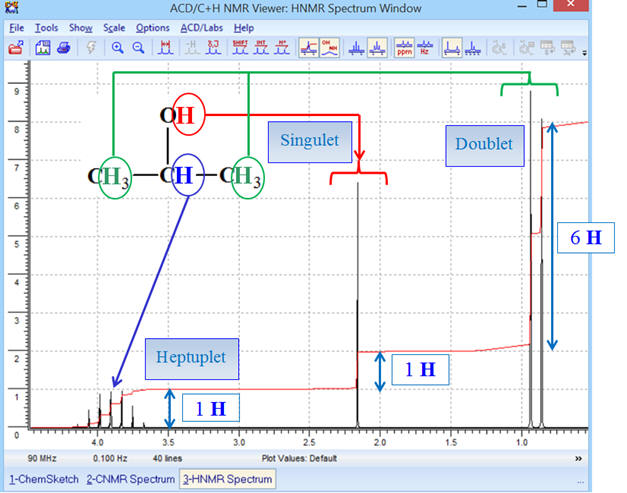
Le signal du groupe (A) (groupe méthyne
 ) est constitué d’un
heptuplet ou septuplet (6 + 1),
) est constitué d’un
heptuplet ou septuplet (6 + 1),
- il possède six protons
équivalents voisins (groupe (C) : 2 groupes méthyle
CH3
–).
- Le signal du groupe (B) (groupe hydroxyle – OH) est constitué d’un singulet (0 + 1).
- De façon générale, il
n’existe pas de couplage entre le proton du groupe hydroxyle et les
protons du groupe (A), groupe méthyne
 .
.
- Le groupe signal du (C) (groupe méthyle CH3 –) est constitué d’un doublet (1 + 1).
- Il possède 1 proton
équivalent voisin : groupe méthyne (A)
 .
.
-
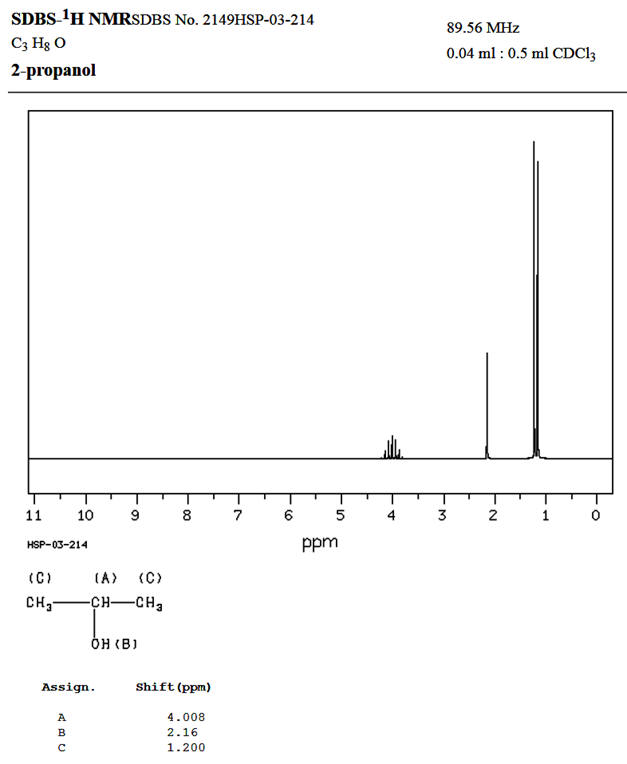
Spectre donné par le
site SDBS-1HNMR :
-
Comparaisons :
|
|
|
Groupe (A) |
Groupe (B) |
Groupe (C) |
|
Spectre obtenu |
Déplacement
chimique (ppm) |
3,9 |
2,16 |
0,9 |
|
Nombre de
pics
du signal |
7 |
1 |
2 |
|
|
Site
SDBS-1HNMR |
Déplacement
chimique (ppm) |
4,008 |
2,16 |
1,2 |
|
|
7 |
1 |
2 |
-
Il y a une différence notable au niveau de la valeur du
déplacement chimique du groupe (C).
-
Cela provient du fait que l’on a utilisé la valeur donnée
dans le tableau de données :
|
CH3
– C |
0,9 ppm |
-
En réalité, le décalage est plus important car il y a la
présence de l’atome d’oxygène du groupe hydroxyle (groupe (B).
|
CH3
– C – O |
1,4 ppm |
-
On peut aussi choisir la valeur donnée dans le tableau de
données.
-
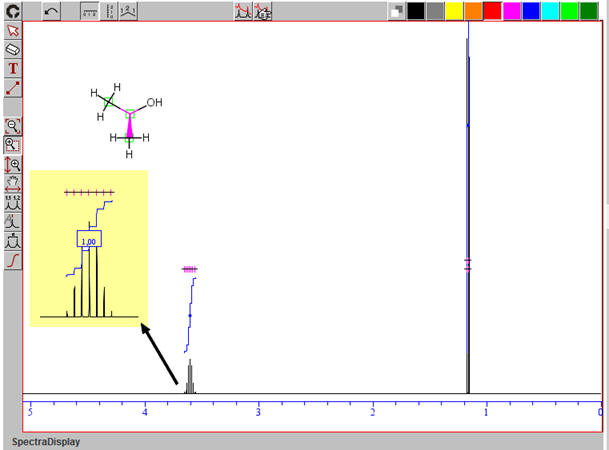
Avec le logiciel de simulation :https://www.nmrdb.org/predictor/
- On remarque que le spectre RMN ne comprend que 2 signaux.
- Il manque le signal relatif au proton du groupe hydroxyle
(singulet à 2,16 ppm).
|
|