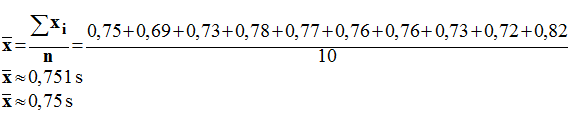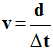Exercices  : énoncé et correction a)- Exercice 5 page 242. Question de référentiel. b)- Exercice 6 page 242. La poursuite par équipe. c)- Exercice 7 page 244. Championnats du monde d’athlétisme. d)- Exercice 12 page 244. La photofinish. e)- Exercice 13 page 244. Prendre un bon départ.

En relation avec Phys. N° 04 La Relativité du Mouvement (à faire sous forme de TP)

 

I- Mouvement dans le sport.

1)- Choix du système étudié.

-  On choisi dans un premier temps, l’objet ou un ensemble d’objets  dont on veut étudier le mouvement.

-  On peut indiquer, la masse m de l’objet,

-  Exemples : un cycliste, un bobsleigh, le ballon d’une gymnaste, un sprinteur,

 

2)- Choix du référentiel d’étude.

-  Le référentiel Terrestre que l’on utilise pour les mouvements à la surface de la Terre.

-  Avant toute étude, il faut préciser le référentiel d’étude.

-  On associe un repère d’Espace lié à ce référentiel Terrestre.

-  Le plus souvent on choisit le repère d’Espace qui permet de simplifier l’étude du mouvement du système choisi.

 

3)- La relativité du mouvement.

-  Exemple : Course cycliste : le Tour de France.

-  Un photographe a réalisé deux photographies d’une course avec le même appareil et les mêmes réglages.

-  Dans un cas, il suit les coureurs dans une voiture avec la même vitesse v.

-  Dans l’autre cas, il et immobile sur le trottoir.

  

-  À quelle situation correspond chacune des photos ?

-  La photo 1 correspond au cas où le photographe est immobile sur le trottoir.

-  Le référentiel d’étude est le photographe, il est immobile par rapport à la Terre.

-  Le référentiel dans ce cas est un référentiel terrestre.

-  Les coureurs se déplacent à la vitesse v.

-  Avec les réglages de l’appareil photo, ils apparaissent flous.

-  Il faut dans ce cas raccourcir la durée de prise de vue.

-  On peut remarquer que les autres spectateurs qui sont sur le trottoir et qui sont immobiles par rapport au photographe ne sont pas flous.

-  La photo 2 correspond au cas où le photographe est dans une voiture ou sur une moto.

-  Le référentiel d’étude dans ce cas est la voiture ou la moto.

-  Avec les réglages de l’appareil, les cyclistes ne sont pas flous car ils sont immobiles par rapport à la voiture.

-  Alors que les spectateurs qui sont sur le trottoir sont flous car ils se déplacent à la vitesse v par rapport à la voiture.

-  Dans la première situation, l’appareil photo correspond à un référentiel terrestre.

-  Suivant le référentiel d’étude, un objet dont on étudie le mouvement peut être immobile ou en mouvement.

II- Le chronométrage.

1)- Historique :

►  1862 : chronographe à aiguilles,  précision : 1/5^e de seconde.

►  1912 : chronographe à aiguilles,  précision : 1/10^e de seconde.

-  L’œil humain ne peut distinguer séparément deux évènements que s’ils sont séparés d’au moins 1/10^e de seconde.

-  C’est donc la meilleure  précision que l’on peut obtenir avec un chronométrage manuel.

►  1902 : premiers enregistrements électriques précis au 1/100^e de seconde.

-  Ils sont utilisés aux Jeux de Los Angeles en 1932.

-  Les performances restent affichées au 1/10^e de seconde.

-  La précision de l’enregistreur au 1/100^e ne sert qu’à départager les coureurs qui arrivent dans le même dixième.

►  1952 : affichage au 1/100^e de seconde au Jeux d’Helsinki.

-  Les trois athlètes qui montent sur le podium ne sont séparés que de 4/100^e de seconde.

►  1967 : Chronométrage au 1/1000^e de seconde.

-  En natation, la mise en place des plaquettes de touche à  l’arrivée, couplées à une vidéo permet d’améliorer grandement la précision.

►  1968 : La photofinish :

-  Le système deviendra officiel en 1968.

-  Depuis 1973, on sait mesurer les records sportifs au 1/10000^e de seconde

►  2000 : à Sydney, les caméras étaient capables de fournir en moins de 15 s :

-  La photofinish du vainqueur,

-  Son temps personnel,

-  La vitesse du vent,

-  Le temps de réaction au starter.

-  Photofinish de la finale du 100 m des Jeux de 2008

Cliquer sur l'image pour l'agrandir 

2)- Exemple :

►  Comment chronométrer le plus précisément possible la durée d’un parcours ?

-  Pour simuler une descente en bobsleigh, on utilise une balle qui descend sur un plan incliné.

-  La balle a été lâchée d’un point O sans vitesse initiale.

-  On a tracé deux repères A et B sur le parcours.

 

  Première méthode :

On dispose d’un chronomètre manuel.

-  On déclenche le chronomètre lors du passage de la bille devant le repère A et on arrête le chronomètre lorsque la bille passe devant le repère B.

-  On réalise 10 fois la même expérience dans les mêmes conditions.

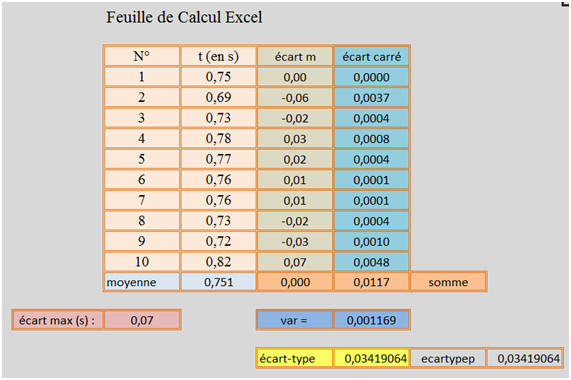
-  On obtient les résultats suivants :

-  Déterminer la valeur de la moyenne de ces mesures.

-  Quel est l’écart maximal par rapport à la valeur de la moyenne.

-  Déterminer la valeur de l’écart-type de cette série de mesures.

-  Conclusions.

-  Valeur de la moyenne arithmétique : t_m ≈ 0,75 s et écart-type : σ ≈ 0,036 s

-  Moyenne arithmétique :

-  La moyenne arithmétique est le quotient de la somme des valeurs x _i par le nombre total de valeurs de la liste est n.

-    On écrit :

-  Écart à la moyenne de chacune des valeurs :

-  Notation : l’écart à la moyenne de chacune des valeurs est noté :

-  On remarque que l’écart maximal est de 0,07 s par rapport à la moyenne.

-  La variance var est le quotient de la somme des carrés des écarts à la moyenne par le nombre n de l’effectif total.

-   

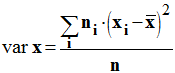
-  Calculer la variance de l’échantillon.

-  var  ≈  0,001169 s²

-  var  ≈  0,0012 s²

-  L’écart type σ :

-  L’écart-type σ est égal à la racine carrée de la variance.

-  L’écart-type caractérise la dispersion des valeurs.

-  Affirmation :

-  En mathématique, on constate que l’intervalle  contient plus de la moitié des valeurs de la liste.

-  Valeur de l’écart-type :

-   

-  L’expérience est réalisée plusieurs fois dans les mêmes conditions pour vérifier la reproductibilité et éviter les erreurs grossières.

-  On remarque que les valeurs sont assez dispersées.

-  On ne peut pas espérer atteindre une grande précision avec cette méthode.

-  On peut l’améliorer en plaçant des repères pour mieux apprécier le passage devant A et B.

-  Ici, on n’est plus limité par la précision du chronométreur que par la précision du chronomètre.

 

  Deuxième méthode :

On dispose d’un chronomètre et de capteurs électroniques pour déclencher et arrêter automatiquement le chronomètre au passage de la balle en A et B.

 

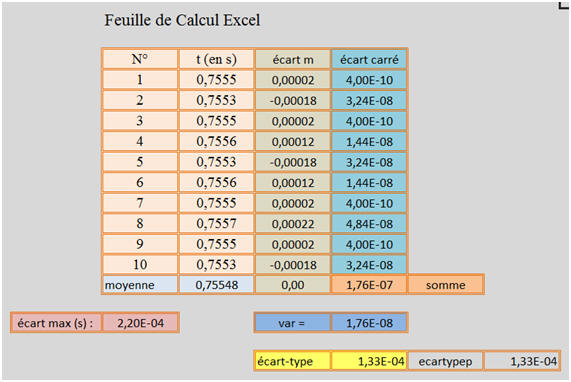
-  On réalise 10 fois la même expérience dans les mêmes conditions. On obtient les résultats suivants :

-  Déterminer la valeur de la moyenne de ces mesures.

-  Quel est l’écart maximal par rapport à la valeur de la moyenne.

-  Déterminer la valeur de l’écart-type de cette série de mesures.

-  Conclusions.

 

-  La valeur moyenne  t_m ≈ 0,755 s.

-  Avec un écart maximal de 0,0002s par rapport à la moyenne.

-  Les valeurs sont beaucoup moins dispersées.

-   L’écart-type σ ≈ 0,00013 s. 

-  La moyenne des valeurs, t_m ≈ 0,755 s, peut être donnée avec davantage de chiffres significatifs.

-  La mesure est plus précise.

-  L’utilisation de capteurs électroniques permet de réduire l’erreur au déclenchement et à l’arrêt du chronomètre.

III- La description du mouvement.

1)- La trajectoire.

-  Dans un référentiel donné, la trajectoire d’un point du système étudié est l’ensemble des positions successivement occupées par ce point au cours du mouvement.

-  La trajectoire d’un point du système étudié dépend du référentiel d’étude.

2)- La valeur de la vitesse.

-  Dans un référentiel donné, la valeur de la vitesse v d’un point du système étudié est définie par le rapport de la distance parcourue d par la durée Δt du parcours :

3)- La nature du mouvement.

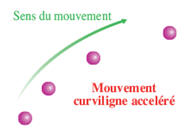
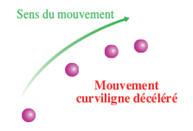
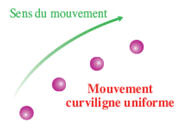
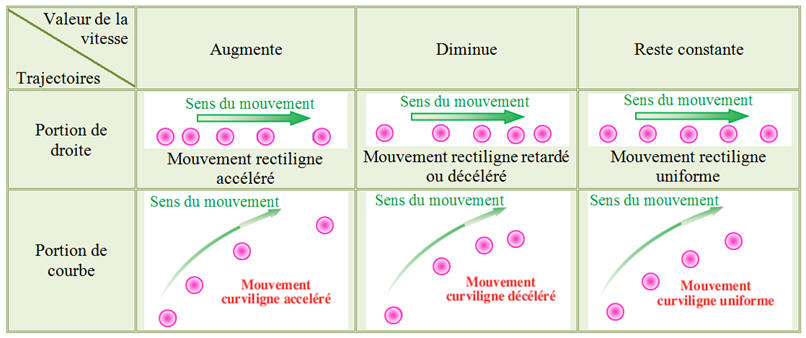
-  Dans un référentiel donné, les caractéristiques du mouvement d’un point du système étudié dépendent de la  forme de la trajectoire et de l’évolution de la valeur de sa vitesse.

 

IV- Applications :

1)- QCM : Pour chaque question, indiquer la (ou les) bonne(s) réponse(s).

QCM sous forme de tableau 01 QCM sous forme de tableau 02 QCM sous forme de tableau 03  QCM Questy 01  QCM Questy 02  QCM Questy 03

2)- Exercices :

a)- Exercice 5 page 242. Question de référentiel.

b)- Exercice 6 page 242. La poursuite par équipe.

c)- Exercice 7 page 244. Championnats du monde d’athlétisme.

d)- Exercice 12 page 244. La photofinish.

e)- Exercice 13 page 244. Prendre un bon départ.