I-  Chute d’une bille dans l'huile. 1)- Protocole expérimental. 2)- Récupération des mesures. 3)- Traitement des mesures. 4)- Étude dynamique. II- Étude énergétique. Conclusions

I-  Chute d’une bille dans l'huile. Autre étude : Chute verticale dans un fluide.

Pour aller plus loin

1)- Protocole expérimental.

-     On filme, à l’aide d’une WebCam la chute d’une bille dans l’huile contenue dans une éprouvette graduée de 1 L.

-   On obtient le fichier : bille50. bille50.zip

-     Ouvrir le logiciel d’acquisition et de traitement vidéo : aviméca 2.7.

-     Clique sur l’icône : et dans le dossier vidéoS, choisir le fichier : bille50. Vidéo : bille50.zip

-     Avant d’effectuer les mesures, cliquer sur l’icône  et choisir 200 % pour agrandir l’image et améliorer la précision.

-     Cliquer sur l’icône : propriétés du clip et les noter.

-     Propriétés du clip :

 

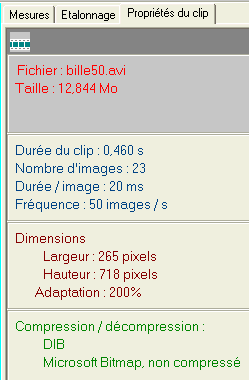
-     Cliquer sur l’icône étalonnage :

-     Remarque : Ne pas oublier de choisir l’origine des axes.

-   On peut choisir l’origine des axes après avoir effectué les mesures.

Données :

Rayon de la bille : r = 5,00 mm	Masse de la bile m = 4,08 g
Masse volumique de la bille ρ = 7563 kg.m– 3	Masse volumique de l’huile ρ 0 = 920 kg.m– 3
Distance (graduations 50 mL et 500 mL) : D = 242 mm	Intervalle de temps entre 2 images : τ = 20 ms

2)- Récupération des mesures.

-     Cliquer sur l’icône : .

-   Il apparaît l’affichage suivant :

-     Cliquer sur OK.

-   Les valeurs sont dans le presse-papier. Il ne reste plus qu’à les exploiter.

-     Ouvrir une feuille de calcul Excel, sélectionner la cellule B3 et cliquer sur ‘’coller’’.

-     Pointage vidéo :

 

3)- Traitement des mesures.

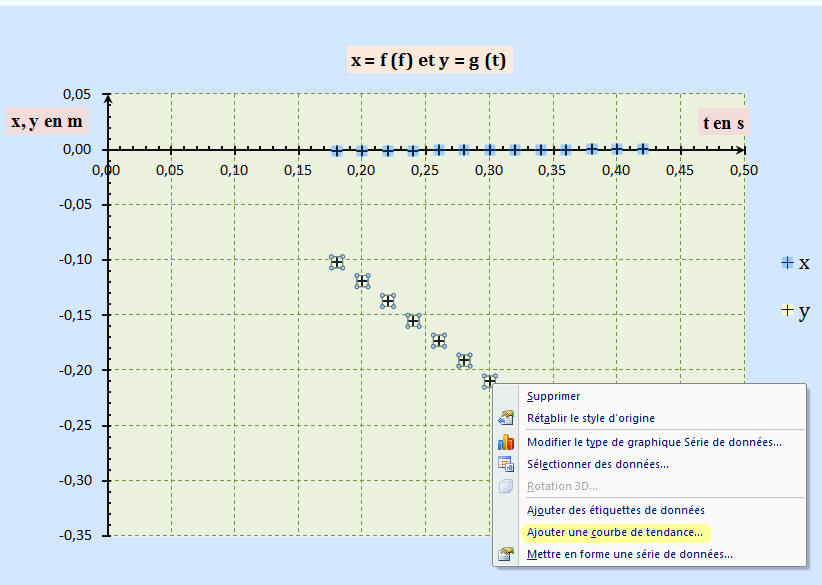
a)-   Représenter sur le même graphique : x = f (t) et y = g (t). Commenter les courbes obtenues.

-     Graphe 01 : x = f (t) et y = g (t)

 

-     Étude de x = f (t) et y = g (t) :

-     On peut écrire que x = 0, l’abscisse de la bille ne varie pas au cours du temps.

-     D’autre part : y = g (t), l’ordonnée varie au cours du temps.

-     On en déduit que la chute de la bille se fait suivant la verticale du lieu.

-     On remarque que pour t ≥ 0,18 s, les points sont sensiblement alignés.

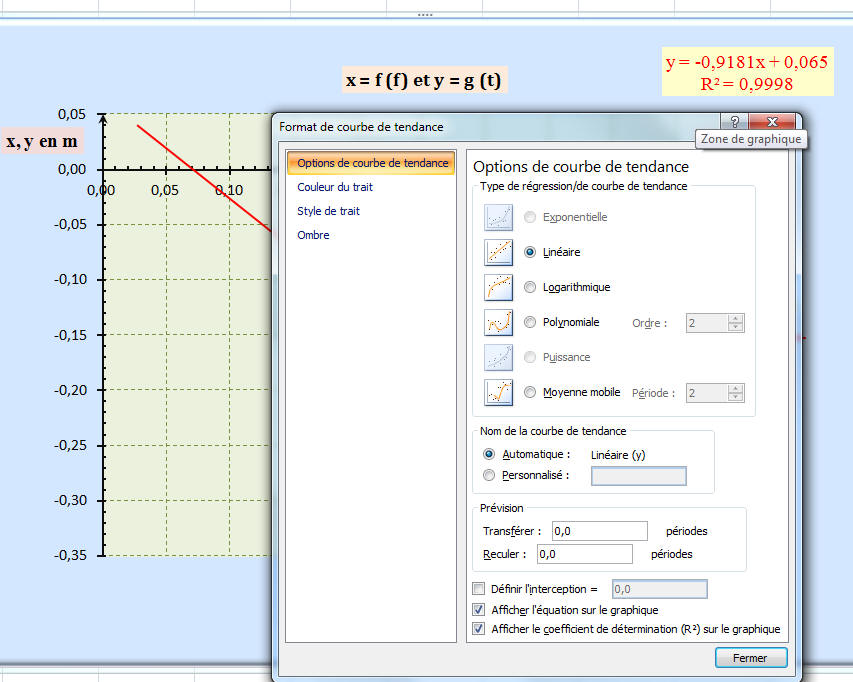
-     Pour faire l’étude avec le logiciel Excel, on supprime les 8 premières images.

-     On obtient le graphe suivant :

 

-      On sélectionne les données, puis on fait un clic droit et on choisit :

-   Ajouter une courbe de tendance.

 

-     Puis sélectionner « Linéaire » pour le type de régression de la courbe de tendance.

-     Ne pas oublier de cocher les options :

-     « Afficher l’équation sur le graphique » et « Afficher le coefficient de détermination (R²) sur le graphique ».

 

-     Le logiciel affiche comme équation : y = – 0,9181 x + 0,065

-     La traduction physique de cette équation après avoir arrondi donne :

-     Équation : y = – 0,92 t + 0,065

-     L’ordonnée est une fonction affine du temps lorsque t ≥ 0,18 s.

-     On en déduit que pour t ≥ 0,18 s, le mouvement de la bille est vertical et uniforme.

b)-  Dans quel référentiel étudie-t-on le mouvement de la bille ?

-     Référentiel d’étude :

-     Le mouvement de la bille est étudié dans le référentiel lié à l’éprouvette, c’est-à-dire un référentiel terrestre.

c)-   Décrire le mouvement de la bille dans ce référentiel.

-     Mouvement de la bille dans ce référentiel :

-     Le mouvement de la bille est rectiligne.

-     Il comporte deux phases.

-     Une première phase ou la vitesse de la bille augmente, le mouvement est accéléré.

-     Une deuxième phase où la bille parcourt des distances égales pendant des durées égales, le mouvement est uniforme

d)-  Déterminer la valeur de la vitesse moyenne v_moy de la bille entre les deux positions extrêmes.

-     vitesse moyenne v _moy de la bille entre les deux positions extrêmes.

-      

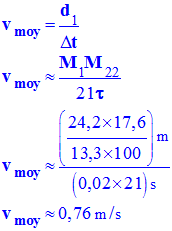
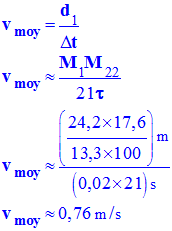
e)-   Déterminer la valeur de la vitesse instantanée aux temps t₈ et temps t₁₄. Décrire la méthode utilisée.

-     valeur de la vitesse instantanée aux temps t₈ et temps t₁₄.

-      

-      

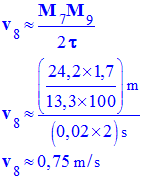
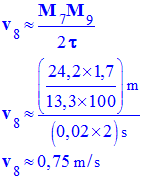
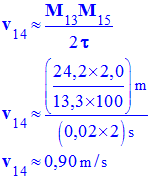
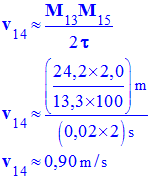
-     Pour calculer la valeur de la vitesse à un instant donné, on calcule la valeur vitesse moyenne pendant un intervalle de temps très court encadrant l’instant considéré.

-     Comme ici, la vidéo comporte 50 images par seconde.

-     On choisit l’image avant et l’image après la position étudiée : 0,040 s

f)-   Comment peut-on faire pour connaître la valeur de la vitesse à chaque instant à l’aide du tableur.

-     Calcul de la valeur de la vitesse instantanée avec le tableur :

-     Pour connaître la valeur de la vitesse à chaque instant à l’aide du tableur, on calcule la vitesse moyenne pendant un intervalle de temps très court encadrant l’instant considéré :

 

-     Comme vitesse initiale, on choisit v₀ = 0,0 m / s car la bille est immobile à l’instant t = 0 s.

-     Pour calculer la valeur de la vitesse du point N° 1, on utilise la méthode déjà utilisée :

-     On calcule la vitesse moyenne pendant un intervalle de temps très court encadrant l’instant considéré :

-     On tape la formule suivante dans la cellule E7 : = ABS(D8 – D6) / 0,04

-     Le signe égale : pour signifier à Excel que l’on tape une formule

-     ABS () car on calcule la valeur de la vitesse qui est une grandeur positive

-     L’intervalle de temps vaut 2 t = 40 ms.

-     On recopie cette formule vers le bas autant que nécessaire avec la souris (copier – glisser) (jusqu’à la case E26)

-     Tableau de valeurs :

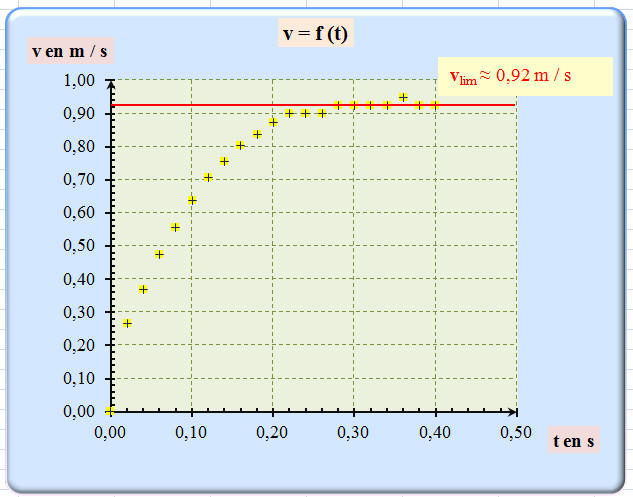
g)-  Représenter v = f (t). Commenter la courbe obtenue. En déduire la valeur de la vitesse limite v_lim.

-     Représentation de v = f (t)

 

-     Le mouvement de la bille comporte deux phases.

-     Une première phase (0,0 s ≤ t ≤ 0,18 s) où la vitesse de la bille augmente, le mouvement est accéléré.

-     Une deuxième phase (t ≥ 0,18 s) où la bille parcourt des distances égales pendant des durées égales, le mouvement est uniforme.

-     Valeur de la vitesse limite v_lim :

-     Première méthode : On peut faire une détermination graphique :

 

h)-  Déterminer la valeur v_lim de cette vitesse limite par une autre méthode. Pourquoi la bille atteint-elle une vitesse limite ?

-     Deuxième méthode : On calcule la vitesse moyenne entre t₁₂ et t₂₂ {mouvement rectiligne uniforme : v_moy = v (t)

-      

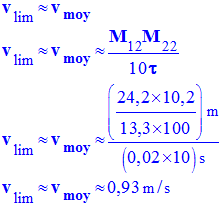
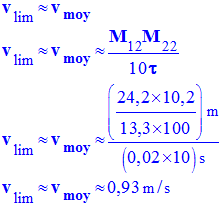
-     Troisième méthode : On calcule la vitesse instantanée :

-      

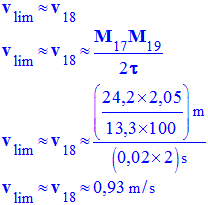
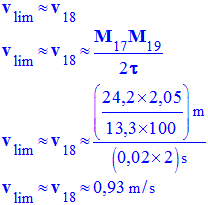
-     La bille atteint une vitesse limite car il existe des forces de frottements fluides.

-     Les forces de frottements dans un liquide visqueux sont plus importantes que dans l’air.

-  Très vite, la bille atteint une vitesse limite.

4)- Étude dynamique. Le système étudié est la bille.

a)-   Faire le bilan des forces extérieures appliquées au système au temps t = 0 s, puis aux temps t₁, t₂, ….

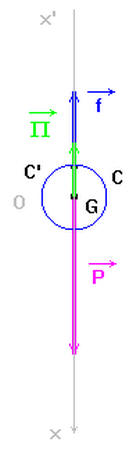
-     Bilan des forces au temps t = 0,0 s.

-     Le poids  et la poussée d’Archimède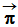

-     Bilan des forces pour t > 0,0 s.

-     Le poids 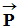, la poussée d’Archimède 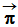 et la force de frottement .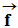

b)-  Décrire le mouvement de la bille entre t₀ et t₈, puis entre t₈ et t₂₁. Quelles conclusions peut-on tirer ?

-     Mouvement de la bille entre t₀ et t₈

-     La vitesse de la bille augmente, le mouvement est accéléré.

-     Les forces n’ont pas des effets qui se compensent.

-     Mouvement de la bille entre t₈ et t₂₁

-     La vitesse de la bille n’augmente plus, le mouvement est rectiligne uniforme.

-     Les forces ont des effets qui se compensent.

II- Étude énergétique.

     Représenter sur le même graphique les variations de l'énergie cinétique, de l'énergie potentielle et de l'énergie mécanique en fonction de t.

     Donner l'allure du graphique observé et tirer les conclusions des observations faites.

-     Tableau de valeurs :

-     Graphe :

 

-     On remarque qu’au cours de la chute de la bille :

-      L’énergie cinétique du système augmente puis se stabilise.

-      L’énergie potentielle de pesanteur diminue.

-     L’énergie mécanique du système diminue aussi.

-     En conséquence, l’énergie mécanique de la bille ne se conserve pas.

►    Conclusions :

-     Un solide en chute dans un fluide est soumis à des frottements exercés par le fluide.

-     Son énergie mécanique diminue au cours de la chute.

-     De l’énergie est transférée de la bille vers le fluide.

-     Lorsqu’un solide chute avec frottements, une partie de son énergie mécanique est :

-     Soit transférée à un autre système,

-     Soit transformée en une autre forme d’énergie.

-     Ceci découle du principe de conservation de l’énergie.