QCM réalisé avec Questy (pour s'auto-évaluer) QCM sous forme de tableau

 

Exercices :   énoncé avec correction a)-  Exercice 8 page 55. Exploiter la relation entre fréquence et longueur d’onde b)-  Exercice 10 page 55. Comprendre et exploiter la loi de Wien. c)-  Exercice 13 page 55. Calculer des énergies et des longueurs d’onde. d)-  Exercice 14 page 55. Exploiter un diagramme d’énergie. e)-  Exercice 17 page 56. Lampe à vapeur de sodium. f)-  Exercice 19 page 56. Spectre d’Arcturus. g)-  Exercice 23 page 58. Vérifier la loi de Wien.

I- Les différentes sources lumineuses.

1)- Introduction.

On distingue :

►  Les sources chaudes dont l’émission de lumière est d’origine thermique :

-  Le Soleil, les lampes à incandescence, les lampes halogènes, la flamme d’une bougie, …

►  Les sources froides dont l’émission de lumière à lieu sans échauffement :

-  Le tubes fluorescents, lampes fluo-compactes, les lasers, les diodes électroluminescentes, …

2)- Dispersion de la lumière blanche par un prisme.

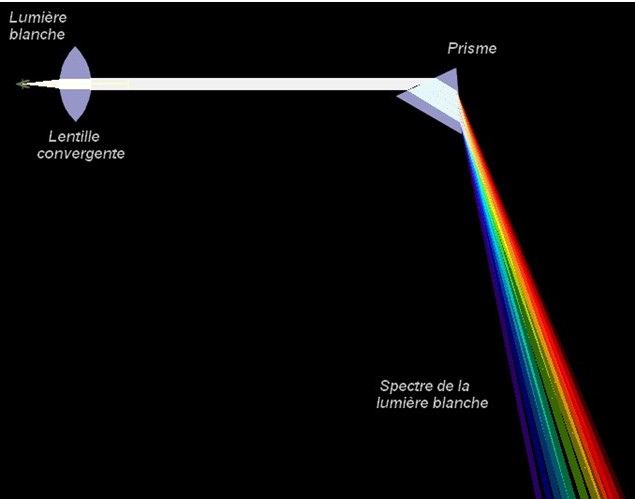
a)-  Expérience de Newton (1642 – 1727).

  Expérience : on éclaire une fente avec une lumière blanche et on envoie le faisceau obtenu sur la face d’un prisme.

 

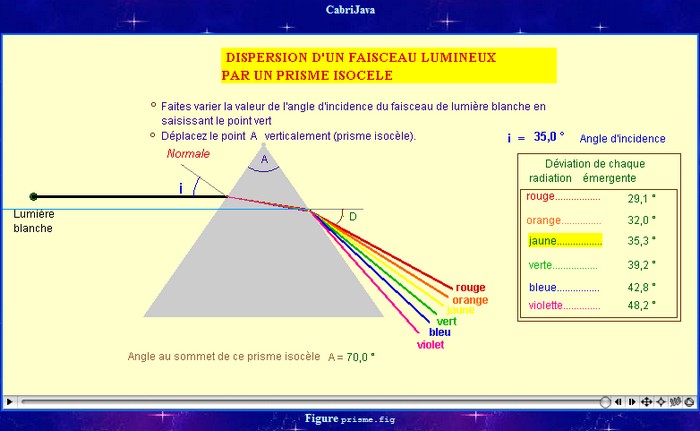
Animation CabriJava : déviation par un prisme

 

 

Spectre de la lumière blanche :

 

-  Observations :

-  La lumière est déviée par le prisme.

-  De plus le faisceau qui émerge du prisme est étalé et présente les différentes couleurs de l’arc-en-ciel (rouge, orange, jaune, vert, bleu, indigo, violet).

-  La lumière rouge est moins déviée que la lumière violette.

  Conclusion 1 :

-  Le prisme dévie et décompose la lumière blanche en lumières colorées du rouge au violet.

-  C'est un phénomène de dispersion.

-  L'ensemble des couleurs obtenues constitue le spectre de la lumière blanche.

-  Le spectre est continu du rouge au violet.

-  La lumière blanche est constituée de plusieurs couleurs ou radiations : c’est une lumière polychromatique.

►  Exemple : Arc en Ciel :

 

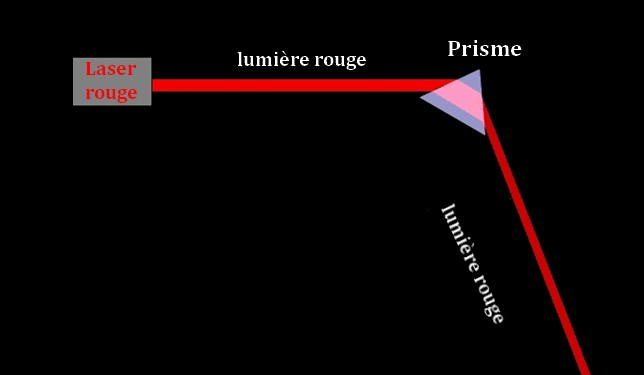
b)-  Expérience avec la lumière émise par un Laser.

  Expérience : on éclaire une fente avec un faisceau laser et on envoie le faisceau obtenu sur la face d’un prisme.

-  Observation :

-  Le faisceau laser est dévié et le spectre ne comporte qu’une seule couleur, la couleur rouge initiale.

 

Spectre du faisceau laser

 

  Conclusion 2 :

-  La lumière produite par un laser est constituée d’une seule radiation, elle est monochromatique.

  Conclusion 3 :

-  Il existe les sources monochromatiques qui émettent une seule radiation lumineuse et les sources polychromatiques qui émettent plusieurs radiations lumineuses.

c)-  Radiation et longueur d’onde.

-  Une lumière monochromatique ne peut être décomposée par un prisme.

-  C’est une radiation lumineuse qui est caractérisée par sa longueur d’onde λ₀ dans le vide ou l’air.

-  Son unité légale est le mètre (m). On utilise souvent le nanomètre (nm) pour les radiations lumineuses

-  Le laser rouge utilisé au lycée est une radiation de longueur d’onde λ = 633 nm.

-  C’est une lumière monochromatique.

-  Remarque : une lumière complexe est un mélange de plusieurs radiations.

-  Elle n’est pas caractérisée par une longueur d’onde.

-  On lui associe une plage de longueurs d’onde.

  Une radiation lumineuse est caractérisée par :

-  Sa fréquence ν (en Hz) ou sa période T (en s)

-  Et

-  Sa longueur d’onde dans le vide λ₀.

-  Remarque :

-  La fréquence ν d’une radiation lumineuse ne dépend pas du milieu de propagation alors que la longueur d’onde λ dépend du milieu de propagation.

-  Les radiations lumineuses sont des ondes électromagnétiques.

  Relation fondamentale :

-  La longueur d’onde dans le vide d’une radiation lumineuse est donnée par la relation :

-  Remarque : Pour les radiations lumineuses, on préfère utiliser la lettre grecque ‘’nu’’.

-  De manière générale, on caractérise une radiation lumineuse par sa longueur d’onde dans le vide λ₀.  

-  Le plus souvent, lorsque l’on donne la longueur d’onde d’une radiation, il est sous-entendu que c’est celle dans le vide ou dans l’air.

d)-  Domaine du visible.

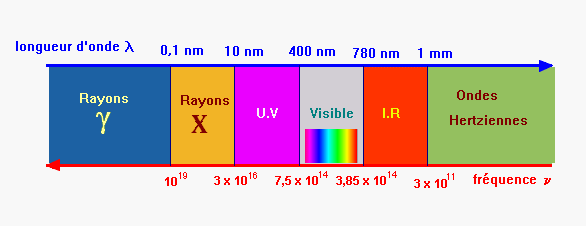
- L’œil humain n’est sensible qu’aux radiations dont les longueurs d’onde sont comprises entre 400 nm et 800 nm.

 

- La lumière blanche est un mélange de toutes les radiations visibles.

II- Lumière émise par une source chaude.

1)- Le profil spectral.

-  Le profil spectral, d’un corps, représente l’intensité lumineuse des radiations émises par ce corps en fonction des longueurs d’onde de ces radiations.

-  Le profil spectral d’un corps chaud dépend de sa température.

-  La couleur d’un corps chaud dépend de sa température.

-  Exemples : on donne le profil spectral d’un corps chaud à deux températures différentes.

 

Spectre de la lumière émise

 

 

Spectre de la lumière émise

 

-  Les températures sont données en kelvin (K) qui est la température absolue :

-  Relation entre degré Celsius et kelvin :

-  T (K) = θ (° C) + 273,15  

-  On remarque que le spectre d’un corps incandescent dépend de la température de ce corps.

-  Plus le corps est chaud et plus le spectre s’étend vers le violet.

-  En conséquence, une source de couleur bleue est plus chaude qu’une source de couleur rouge.

2)- Loi de Wien. Voir : Exercice 14 : Lien :

Loi de Wien Cours de seconde, vers exercice.

-  Un corps chaud émet de la lumière dont le spectre et le profil spectral dépendent de la température.

-  En physique, un « corps noir » est un objet idéal émettant un rayonnement qui n’est fonction que de sa température.

-  La loi de Wien relie la température θ de ce corps noir et la longueur d’onde λ _max pour laquelle le profil spectral de la lumière qu’il émet passe par un maximum.

-  La température θ s’exprime en degré Celsius et la longueur d’onde λ _max en nm.

-  Ces deux grandeurs sont liées par la loi de Wien :

-   

-  Cette loi permet d’évaluer la température d’une étoile à partir de son profil spectral.

-  Exemple :

-  On donne le profil spectral d’une étoile.

-  En déduire la température de la surface de cette étoile à partir de son profil spectral

 

- 

-  La température de surface du corps chaud est d’environ 6000 °C.

-  La loi de Wien permet d’évaluer la température de surface θ en °C d’un corps chaud à partir de la connaissance de la longueur d’onde λ _max en nm de la radiation émise avec le maximum d’intensité.

III- Lumière émise par une source froide.

1)- Le photon.

-  En 1900, Max Planck fut conduit à postuler la quantification de l’énergie transportée par les ondes électromagnétiques.

-  Il postule que l’énergie électromagnétique ne peut s’échanger que par « paquets » ou quanta d’énergie.

-  En 1905, Albert Einstein émet l’idée que ces quanta d’énergie sont transportés par des photons.

-  Les photons sont des particules de masse nulle et de charge nulle se propageant à la vitesse de la lumière.

-  Énergie d’un photon :

-  E = h . ν ou

-  Pour une onde électromagnétique de fréquence ν et de longueur d’onde λ dans le vide

-  La grandeur h est la constante de Planck : h = 6,62 × 10 ^{– 34} J.s.

-  La grandeur c représente la valeur de la vitesse de la lumière dans le vide :

-  c = 3,00 x 10 ⁸ m / s

-  Autre écriture : .

-  L’énergie E s’exprime en joule.

-  Comme les valeurs des énergies des atomes, exprimées en joule (J) sont extrêmement faibles, on préfère utiliser le plus souvent comme unité d’énergie, l’électron-volt (eV)

-  Correspondance : 1 eV = 1,6 × 10 ^{– 19} J

2)- Quantification de l’énergie des atomes.

-  En 1913, BOHR énonce les postulats suivants :

-  Les variations d’énergie d’un atome sont quantifiées.

-  L’atome ne peut exister que dans certains états d’énergie ou niveaux d’énergie bien définis.

-  Un photon de fréquence ν est émis lorsque l’atome effectue une transition d’un niveau d’énergie E_p vers un niveau inférieur E_n tel que : 

-  E_p - E_n = h . ν

-  Il résulte de ceci que les énergies d’un atome sont quantifiées.

-  Le diagramme des niveaux d’énergie d’un atome représente les niveaux d’énergie possibles de cet atome.

-  Exemple :

-  Diagramme simplifié des niveaux d’énergie de l’atome d’hydrogène (tous les états excités ne sont pas représentés).

-  L’état de plus basse énergie correspond à l’état fondamental.

-  Dans l’état fondamental, n = 1 : E ₁ = - 13,6 eV

-  Les autres états sont qualifiés d’états excités. Il en existe une infinité.

-  Lorsque E = 0, l’atome est ionisé.

-  Dans ce cas, l’atome d’hydrogène a perdu son électron. On est en présence d’un proton.

3)- Émission de lumière.

-  La perte d’énergie d’un atome excité passant du niveau d’énergie E_p vers un niveau inférieur E_n s’accompagne de l’émission d’un photon d’énergie :

-  ΔE = E_p - E_n = h . ν

►  Application :

-  On donne une partie du diagramme des niveaux d’énergie de l’atome d’hydrogène.

 

-  Calculer la longueur d’onde λ₃₁ du photon émis au cours de la transition du niveau 3 au niveau 1.

-  Calculer la longueur d’onde λ₃₂ du photon émis au cours de la transition du niveau 3 au niveau 2.

►  Réponses :

-  Longueur d’onde λ ₃₁ du photon émis au cours de la transition du niveau 3 au niveau 1.

-   

-  Application numérique :

-   

-  Cette radiation n’est pas visible. Elle appartient au domaine des UV.

-  Longueur d’onde λ₃₂ du photon émis au cours de la transition du niveau 3 au niveau 2.

-   

-  Application numérique :

-   

-  Cette radiation appartient au domaine du visible. Elle est de couleur rouge.

 

4)- Absorption de lumière.

-  L’absorption d’énergie lumineuse par un atome ne peut se faire que si l’énergie du photon permet une transition d’un niveau E_n à un niveau supérieur E_p tel que :

-  ΔE = E_p - E_n = h . n

-  Un atome ne peut absorber que les radiations qu’il est capable d’émettre.

►  Application :

-  On donne une partie du diagramme des niveaux d’énergie de l’atome d’hydrogène.

 

-  Calculer la longueur d’onde λ₂₁ du photon absorbé au cours de la transition du niveau 1 (état fondamental) au niveau 2.

►  Réponse :

-   

-  Application numérique :

-   

-  Cette radiation n’est pas visible. Elle appartient au domaine des UV.

IV- Interprétation du spectre de la lumière du Soleil.

1)- Étude du spectre solaire.

-  Profil spectral et spectre simplifiée de la lumière émise par le Soleil.

 

-  Le profil spectral d’une étoile est la courbe qui représente l’intensité lumineuse des radiations émises par cette étoile en fonction de la longueur d’onde.

-  Les entités chimiques présentes dans l’atmosphère du Soleil absorbent certaines radiations lumineuses.

-  Ceci se traduit par l’apparition de raies sombres dans le spectre de la lumière émise par le Soleil et par des minima d’intensité lumineuse dans le profil spectral.

-  Les longueurs d’onde correspondantes permettent d’identifier les entités chimiques présentes dans l’atmosphère du Soleil.

2)- Température de la surface du Soleil.

-  La température de surface du Soleil exerce une influence sur l’allure globale du profil spectral.

-  La longueur d’onde du maximum d’intensité lumineuse est notée λ_max.

-  La valeur de λ_max diminue lorsque la température de surface de l’étoile augmente.

-  Une étoile bleue est plus chaude qu’une étoile rouge.

-  Le profil spectral de la lumière émise par le Soleil permet de déterminer la valeur de λ_max.

-  λ_max = 480 nm.

-  Cette valeur permet de déterminer la valeur de la température de la surface du Soleil grâce à la loi de Wien :

-   

-  Cette température est voisine de 5700 °C.

3)- Composition chimique du Soleil.

Lien vers : Applications à l’Astrophysique.

a)-  Spectres d’émission et spectres d’absorption

-  On a vu qu’un atome émet un photon quand il passe d’un niveau d’énergie supérieur E_p à un niveau d’énergie inférieur E_n.

-  Mais, il peut aussi absorber un photon de même énergie lorsqu’il passe du niveau inférieur E_n au niveau supérieur E_p.

-  Cela explique la présence de raies noires dans les spectres d’absorption.

-  Pour une même entité chimique, les raies noires du spectre d’absorption ont les mêmes longueurs d’onde dans le vide que les raies colorées du spectre d’émission.

►  Cas de l’Hydrogène :

-  Spectre d’émission :

 

 

-  Spectre d’absorption :

 

-  Une entité chimique ne peut absorber que les radiations qu’elle est capable d’émettre.

-  Les raies d’émission ou d’absorption permettent d’identifier une entité chimique présente dans un gaz.

b)-  Conclusion.

- Les raies noires présentes dans le spectre de la lumière provenant du Soleil ou les minima d’intensité lumineuse de son profil spectral permettent d’identifier les espèces chimiques présentes dans l’atmosphère solaire. - L’atmosphère du Soleil contient des éléments chimiques. - La partie haute de l’atmosphère absorbe une partie de la lumière émise dans la partie basse. - Il en résulte des raies d’absorption dans le spectre continu. - Ce sont les raies d’absorption des éléments chimiques présents dans l’atmosphère du Soleil. - Si le Soleil ne comportait pas d’atmosphère, le spectre de la lumière émise serait continu. - L’existence des raies d’absorption est dû à la présence d’une atmosphère autour du Soleil, appelée chromosphère. - Le gaz présent est principalement de l’hydrogène. On trouve aussi des ions He+, Ca2+, Fe2+, … - La partie haute de l’atmosphère absorbe une partie de la lumière émise dans la partie basse. - Les travaux de Fraunhofer et Kirchhoff ont permis de connaître la composition de l’atmosphère du Soleil. - Un spectre d’émission ou d’absorption est caractéristique des atomes ou des ions. - Un spectre de raies d’émission ou d’absorption permet d’identifier une entité chimique (atome ou ion). - C’est sa carte d’identité, sa signature. - « dès 1814, le physicien allemand Fraunhofer remarque la présence de raies noires dans le spectre du Soleil. - Kirchhoff mesure la longueur d’onde de plusieurs milliers de ces raies et montre qu’elles coïncident avec celles émises par diverses entités chimiques : - Hydrogène, calcium, cuivre, fer, zinc, … - Il publie, en 1861, le premier atlas du système Solaire. »

V- Applications.

1)- QCM : Pour chaque question, indiquer la (ou les) bonne(s) réponse(s).

QCM réalisé avec Questy (pour s'auto-évaluer) QCM sous forme de tableau

2)- Exercices : Exercices :   énoncé avec correction

a)-  Exercice 8 page 55. Exploiter la relation entre fréquence et longueur d’onde

b)-  Exercice 10 page 55. Comprendre et exploiter la loi de Wien.

c)-  Exercice 13 page 55. Calculer des énergies et des longueurs d’onde.

d)-  Exercice 14 page 55. Exploiter un diagramme d’énergie.

e)-  Exercice 17 page 56. Lampe à vapeur de sodium.

f)-  Exercice 19 page 56. Spectre d’Arcturus.

g)-  Exercice 23 page 58. Vérifier la loi de Wien.