|
Dynamique du dipôle RC Exercices |
|
|
|
|
|
|
QCM r
Dynamique du dipôle RC L’intensité du courant électrique Le condensateur Le modèle du circuit RC série |
1)- Exercice 04 page 436 : Comprendre le fonctionnement d’un condensateur :
|
Comprendre le fonctionnement d’un condensateur : 1.
Identifier les parties conductrices et
isolantes du condensateur schématisé ci-dessous :
2.
Comment la charge électrique évolue-t-elle
si l’intensité du courant est positive ? |
|
Comprendre le fonctionnement d’un condensateur : 1.
Schéma légendé d’un condensateur :
2.
Évolution de l’intensité et de la charge
électrique :
-
Si l’intensité du courant est
positive, la charge qA
est positive et augmente au cours du temps.
- Le signe de l’intensité du courant est lié au sens de variation de qA charge portée par l’armature A et donc de celui de la tension uC
aux bornes du condensateur et inversement.
-
Relation :
-
Si :
-
La grandeur
-
La charge qA est une
fonction croissante
du temps car sa dérivée par rapport au temps est
une grandeur positive. |
2)- Exercice 08 page 437 : Déterminer la capacité d’un condensateur :
|
Déterminer la capacité d’un condensateur : Le graphique ci-dessous représente la charge électrique d’une
armature d’un condensateur en fonction de la tension à ses bornes. 1.
Rappeler la relation liant la charge qA
et tension uAB aux bornes du condensateur et
déterminer sa capacité. 2.
Est-elle d’un ordre de grandeur usuel ? |
|
Déterminer la capacité d’un condensateur :
-
Graphe
qA =
f (uAB) : 1.
Relation liant la charge qA
et tension uAB et capacité du condensateur.
-
Schéma normalisé du condensateur :
-
Relations importantes :
-
La charge
qA portée
proportionnelle à la tension à la tension uAB
= uC aux
bornes du condensateur.
-
La courbe
qA =
f (uAB) est une droite qui passe par l’origine.
-
Elle est du type
y = a .
x
-
La capacité du condensateur et égale
au coefficient directeur de la droite obtenue.
- 2.
Ordre de grandeur de la capacité :
-
L’ordre de grandeur de la capacité du
condensateur est le microfarad (μF).
-
On trouve beaucoup de condensateurs
de ce type dans les circuits électroniques.
-
C’est une valeur usuelle.
|
||||||||
3)- Exercice 10 page 437 : Différencier charge et décharge d’un condensateur :
|
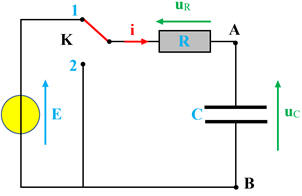
Différencier charge et décharge d’un condensateur : Associer, à chaque position 1 ou 2 de l’interrupteur du schéma ci-dessous, le graphique représentant la tension uC aux
bornes du condensateur en fonction du temps t.
-
Schéma :
-
Graphes : |
Différencier charge et décharge d’un condensateur :
-
Position 1 : Charge du
condensateur.
-
Initialement, le condensateur est
déchargé :
-
À la date t = 0 s, on bascule
l’interrupteur sur la position 1
-
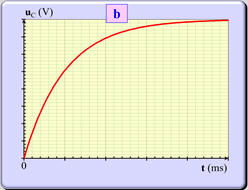
Courbe uC =
f
(t) : Courbe
b
-
La tension uC augmente au cours du temps.
-
Il existe un régime transitoire qui
correspond à la charge du condensateur et un régime permanent
lorsque le condensateur est chargé.
-
Lorsque le condensateur est chargé,
la tension uC
= E
-
C’est la tension délivrée
par le générateur idéal de tension.
-
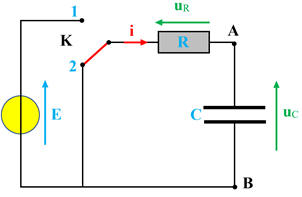
Position 2 : Décharge du
condensateur.
-
Initialement, le condensateur est
chargé : uC =
E
-
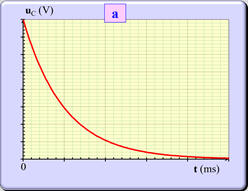
Courbe uC =
f
(t) : Courbe
a
-
La tension uC diminue au cours du temps.
-
Il existe un régime transitoire qui
correspond à la décharge du condensateur et un régime permanent
lorsque le condensateur est totalement déchargé.
-
Lorsque le condensateur est déchargé,
la tension uC ≈
0,0 V
![]()
4)- Exercice 12 page 437 : Établir une équation différentielle :
|
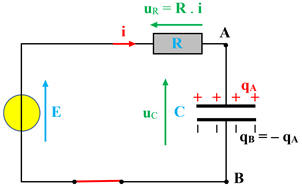
Établir une équation différentielle : Un condensateur préalablement déchargé est placé en série avec un
conducteur ohmique. À la date t = 0 s, l’interrupteur est fermé. Schéma du montage :
1.
Utiliser la loi des mailles pour établir une
relation entre les tensions uC, uR
et E. 2.
Remplacer la tension uR en
utilisant la loi d’Ohm. 3.
Sachant que
aux bornes du condensateur. |
Établir une équation différentielle : 1.
Relation entre les tensions uC,
uR et E.
-
Loi des mailles :
uC+ uR
– E = 0 2.
Loi d’Ohm aux bornes du conducteur ohmique
avec l’orientation choisie :
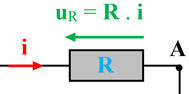
-
Schéma :
-
uR =R
. i 3.
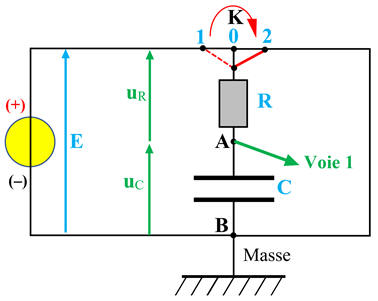
Équation différentielle vérifiée par la
tension uC aux bornes du condensateur.
-
Relations importantes :
uC
Tension aux
bornes du condensateur en volt (V)
qA
Charge de
l’armature A du condensateur en coulomb (C)
i
Intensité du
courant en ampère (A)
C
Capacité du
condensateur en farad (F, μF, nF ou pF)
-
uC+
uR – E =
0
-
E = R . i + uC
avec
-
On en déduit l’équation
différentielle vérifiée par la tension
uC lors de la
charge :
-
►
Solution de l’équation différentielle
vérifiée par la tension uC lors de la charge :
-
Les solutions d’une équation
différentielle y’ = a .
y + b avec
a ≠ 0, sont de la forme :
-
-
La constante
K est liée aux conditions initiales.
-
Les constantes
a et b sont liées aux
caractéristiques du circuit.
-
En utilisant la formulation
précédente :
-
-
Avec comme solution :
-
-
On en déduit que :
-
-
Recherche de l’expression de
K :
-
Au temps
t = 0 s,
uC (0) = 0 le
condensateur est déchargé :
-
-
Solution de l’équation
différentielle :
-
►
Allure de la courbe : cas :
E = 4,0 V ,
R = 1,0 kΩ,
C = 1000 μF
-
Lorsque le condensateur est chargé : - Lorsque le condensateur est chargé,
l'intensité du courant dans le circuit est nulle. - La tension aux bornes du
condensateur est égale à la tesnion E délivrée par
le générateur.
![]()
![]() et
et ![]()
![]()
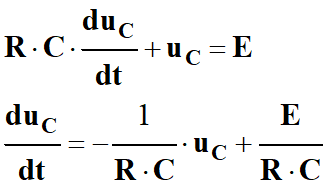
![]()
![]()
![]()
![]()
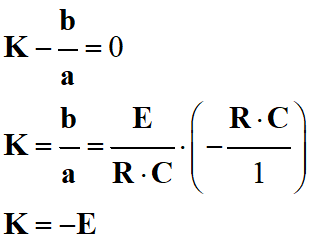
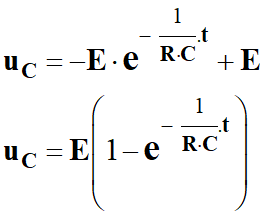
![]()
5)- Exercice 14 page 437 : Résoudre une équation différentielle :
|
Résoudre une équation différentielle :
-
Relier chaque équation différentielle
à sa solution.
|
|
Résoudre une équation différentielle :
-
Équation différentielle et sa
solution :
-
Équation 1 :
-
y’ = 2
y + 3 avec y
(0) = – 1
-
l’équation différentielle est du
type :
-
y’ = a . y +
b avec a ≠ 0,
-
La solution est du type :
-
On en déduit que :
a = 2 et b = 3
-
Détermination de
K à partir des conditions initiales :
-
-
Solution :
-
-
Équation 2 :
-
y’ = 2
y avec y (0) = 5 - l’équation différentielle est du type :
-
y’ = a . y +
b avec a ≠ 0,
-
La solution est du type :
-
On en déduit que :
a = 2 et b = 0
-
Détermination de
K à partir des conditions initiales :
-
y (0) =
K .
e 0 = 5
-
Solution :
-
y = 5 ×
e 2
x
-
Équation 3 :
-
y’ = 2
y + 3 avec y
(0) = 3
-
L’équation différentielle est du
type :
-
y’ = a . y +
b avec a ≠ 0,
-
La solution est du type :
-
On en déduit que :
a = 2 et b = 3
-
Détermination de
K à partir des conditions initiales :
-
-
Solution :
-
-
La valeur de
K est bien liée aux conditions initiales.
-
La grandeur K est liée à la valeur de
y (0).
|
6)- Exercice 15 page 438 : Résoudre une équation différentielle :
|
Résoudre une équation différentielle : L’équation différentielle vérifiée par la tension
uC aux bornes du condensateur chargé à l’aide de la
source idéale de tension E est :
1.
Rappeler la forme des solutions d’une
équation différentielle y’
= a . y +
b avec a ≠ 0. 2.
Par identification, donner la forme des
solutions de l’équation différentielle vérifiée par la tension
uC aux bornes
du condensateur. |
|
Résoudre une équation différentielle :
-
Montage :
-
Équation différentielle :
-
1.
Forme des solutions d’une équation
différentielle y’ =
a . y +
b avec a ≠ 0.
-
Les solutions d’une équation
différentielle y’ =
a . y +
b avec a ≠ 0, sont de la forme :
-
2.
Forme des solutions de l’équation
différentielle vérifiée par la tension
uC aux bornes
du condensateur.
-
Équation différentielle :
-
-
Avec comme solution :
-
-
On en déduit que :
-
-
Forme de la solution :
-
|
7)- Exercice 17 page 438 : Calculer un temps caractéristique :
|
Un dipôle RC série est constitué par l’association d’un
condensateur de capacité C = 47 μF et d’un conducteur ohmique
de résistance R = 1,0 kΩ. 1.
Calculer le temps caractéristique de ce
dipôle. 2.
À partir de la loi d’Ohm et de la relation
|
|
Calculer un temps caractéristique :
-
Un dipôle
RC série :
-
C
= 47 μF et R = 1,0 kΩ.
-
Schéma du montage :
1.
Temps
caractéristique de ce dipôle :
-
τ
= R .
C = 1,0 × 103 × 47 × 10–6
-
τ
≈ 4,7 × 10–2 s
-
τ
≈ 47 ms 2.
Analyse
dimensionnelle de l’expression du temps caractéristique.
-
Loi
d’Ohm : uR = R .
i
-
-
Notations :
-
La
notation [R] représente la grandeur
physique (dans le cas présent la résistance d’un conducteur ohmique.
-
La
notation (Ω) représente l’unité.
-
Ainsi
l’écriture [R] = (Ω) indique que la résistance d’un conducteur ohmique s’exprime
en ohm.
-
Si on
considère le produit R . C :
-
-
De la
relation suivante
-
-
En
conséquence :
-
-
Le produit
(R . C) est bien homogène
à un temps.
-
Il
représente bien le temps caractéristique du dipôle
RC série.
|
8)- Exercice 18 page 438 : Déterminer une capacité par évaluation d’un temps caractéristique :
|
Déterminer une capacité par évaluation d’un temps
caractéristique : Un condensateur de capacité C
inconnue est associé à un
conducteur ohmique de résistance R = 1,0 kΩ. La courbe ci-dessous représente la tension aux bornes du
condensateur en fonction du temps lors de la décharge. Graphe : 1.
Déterminer graphiquement le temps
caractéristique τ de la décharge de ce dipôle. 2.
En déduire la capacité C du
condensateur.
|
Déterminer une capacité par évaluation d’un temps
caractéristique : Graphe : 1.
Détermination graphique du temps
caractéristique τ de la décharge de ce dipôle.
-
Expérience :
-
Montage 1 : E = 4,0 V , R
= 1,0 kΩ, C = ?
-
Initialement, le condensateur est
chargé et l’interrupteur est en position 1 :
-
uC =
E = 4,0 V
-
À la date t = 0 s, on bascule
l’interrupteur sur la position 2.
-
À la voie 1, on enregistre
uC = f (t).
-
On obtient l’enregistrement suivant :
-
Courbe uC =
f (t) :
-
La tension uC
diminue au cours du temps.
-
Lorsque le condensateur est déchargé,
la tension uC ≈
0,0 V
►
Établissement de l’équation
différentielle vérifiée par la tension uC :
-
Loi des mailles (additivité des
tensions) :
-
uR + uC
= 0
-
R . i + uC
= 0 avec
-
On en déduit l’équation
différentielle vérifiée par la tension uC lors de
la décharge :
-
►
Solution de l’équation différentielle
vérifiée par la tension uC lors de la décharge :
-
Les solutions d’une équation
différentielle y’ = a . y + b avec a
≠ 0, sont de la forme :
-
-
La constante K est liée aux
conditions initiales.
-
Les constantes a et b
sont liées aux caractéristiques du circuit.
-
En utilisant la formulation
précédente :
-
-
Avec comme solution :
-
-
On en déduit que :
-
-
Recherche de l’expression de K :
-
Au temps t = 0 s, uC
(0) = E : le
condensateur est chargé :
-
K = E
-
Solution de l’équation
différentielle :
-
-
Dans ce cas :
-
-
Pour déterminer graphiquement la
valeur de τ, on trace la tangente à l’origine à la courbe
uC = f (t).
-
Exploitation graphique :
-
τ ≈ 2,0 ms
-
De plus :
-
-
Ceci est en accord avec le graphe
obtenu. 2.
Capacité C du condensateur.
-
![]()
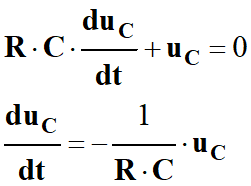
![]()
![]()
![]()
![]()
![]()
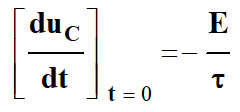
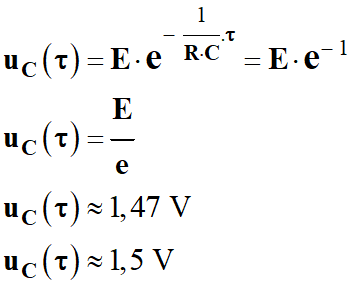
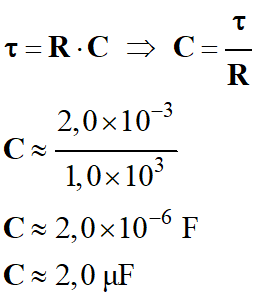
![]()
9)- Exercice 19 page 438 : Flash d’un appareil photographique :
|
Flash d’un appareil photographique :
Un appareil photographique est équipé d’un flash alimenté par une
batterie. Il comporte un circuit électronique dont une partie est
schématisée ci-dessous.
Lors de la prise d’une photographie avec flash, le condensateur emmagasine de l’énergie fournie par la batterie pendant quelques secondes, puis la restitue dans une lampe en 0,10 s. La lampe L émet un éclair lumineux intense. 1.
Sur quelle position faut-il placer
l’interrupteur pour que le condensateur se charge ? 2.
Établir l’équation différentielle vérifiée
par la tension uC aux bornes du condensateur lors
de sa charge. 3.
Résoudre l’équation différentielle et
montrer que
4.
Schématiser le circuit correspondant à la
décharge du condensateur. 5.
Calculer la résistance de la lampe si la
durée Δt nécessaire pour que le condensateur soit déchargé à
99 % est 0,10 s. |
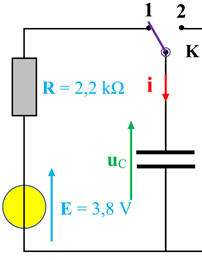
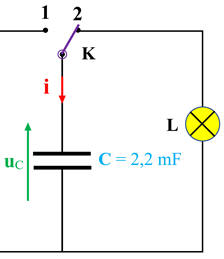
Flash d’un appareil photographique : 1.
Position de l’interrupteur pour que le
condensateur se charge :
-
Il faut mettre l’interrupteur sur la
position 1 :
-
Schéma : 2.
Équation différentielle vérifiée par la
tension uC aux bornes du condensateur lors de sa
charge.
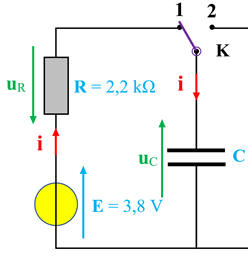
-
Schéma avec orientation choisie et
les différentes tensions :
-
La loi des mailles permet d’écrire la
relation suivante :
-
E –
uR –
uC = 0
-
Or
uR =
R .
i et
-
-
Équation différentielle du type :
-
y’ =
a .
y + b avec
a ≠ 0, 3.
Résolution de l’équation différentielle lors
de la charge.
-
Les solutions d’une équation
différentielle y’ =
a . y +
b avec a ≠ 0, sont de la forme :
-
-
La constante
K est liée aux conditions initiales.
-
Les constantes
a et b sont liées aux
caractéristiques du circuit.
-
En utilisant la formulation
précédente :
-
-
Avec comme solution :
-
-
On en déduit que :
-
-
Recherche de l’expression de
K :
-
Au temps
t = 0 s,
uC (0) = 0 le
condensateur est déchargé :
-
-
Solution de l’équation
différentielle :
-
-
Le produit
R . C représente le temps caractéristique
τ du dipôle RC série :
-
τ
= R . C
-
τ = 2,2 × 103
× 2,2 × 10–3
-
τ ≈ 4,8 s
-
On obtient bien la formulation
suivante :
-
-
-
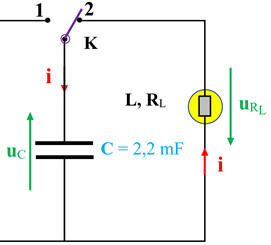
Allure de la courbe : 4.
Schéma du circuit correspondant à la
décharge du condensateur.
-
Circuit de décharge :
-
Au temps
t = 0 s, le condensateur
est chargé, uC
(0) = E, on bascule
l’interrupteur sur la position 2.
-
La lampe émet un flash de lumière. 5.
Résistance de la lampe.
-
Schéma équivalent :
-
Équation différentielle :
-
Loi des mailles :
-
uRL +
uC = 0
-
RL . i + uC = 0 avec
-
On en déduit l’équation
différentielle vérifiée par la tension uC lors de
la décharge :
-
►
Solution de l’équation différentielle
vérifiée par la tension uC lors de la décharge :
-
Les solutions d’une équation
différentielle y’ = a . y + b avec a
≠ 0, sont de la forme :
-
-
La constante K est liée aux
conditions initiales.
-
Les constantes a et b
sont liées aux caractéristiques du circuit.
-
En utilisant la formulation
précédente :
-
-
Avec comme solution :
-
-
Avec :
-
-
Recherche de l’expression de K :
-
Au temps t = 0 s, uC
(0) = E : le
condensateur est chargé :
-
K =
E
-
Solution de l’équation
différentielle :
-
-
-
Le produit
RL .
C représente le temps
caractéristique de l’association série du condensateur de capacité
C et de la lampe de
résistance RL.
-
τ =
RL .
C
-
Durée nécessaire pour que le
condensateur soit déchargé à 99 % :
-
Δt = 5
τ
-
Or, on veut que : Δt = 0,10
s :
-
On en déduit la valeur de la
résistance RL
de la lampe :
-
-
Valeur de la constante de temps :
-
τ ≈ 20 ms
►
Expression de l’intensité du courant
lors de la décharge du condensateur :
-
-
-
-
On remarque que lors de la décharge,
le courant i circule dans
le sens opposé à celui choisi lors de l’orientation du circuit.
-
Allure de la courbe
uC = f (t)
lors de la décharge :
- Dans ce cas :
-
-
Pour déterminer
graphiquement la valeur de
τ,
on trace la tangente à l’origine à la courbe uC =
f (t).
-
Allure de
i =
g (t) et du uC =
f (t) lors de la décharge :
-
Valeur de l’intensité au temps
t = 0 s :
-
![]()
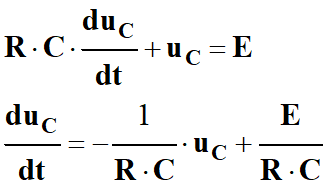
![]()
![]()
![]()
![]()
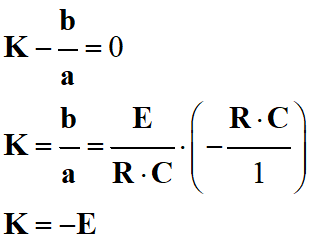
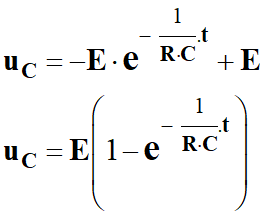
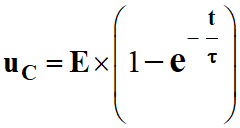
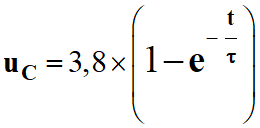
![]()
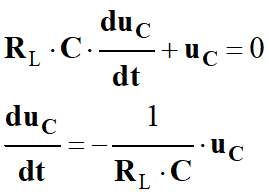
![]()
![]()
![]()
![]()
![]()
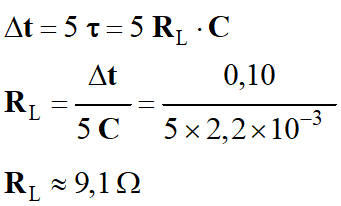
![]() avec
avec ![]()
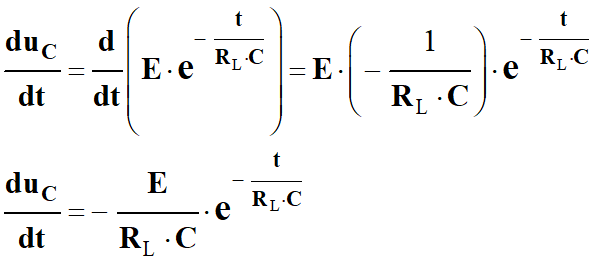
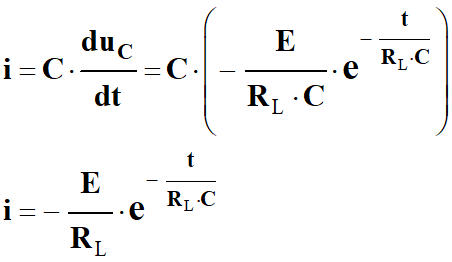
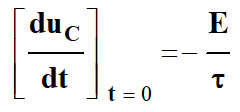
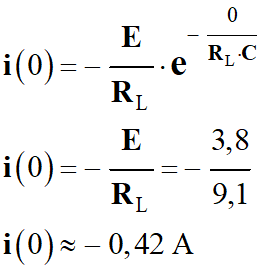
![]()
10)- Exercice 21 page 439 : Caractéristiques d’une pile :
|
Caractéristiques d’une pile : On associe un condensateur préalablement déchargé, de capacité C = 0,10 mF, une pile de force électromotrice E et de
résistance interne r. Dans cette situation, la tension uC aux bornes
du condensateur en fonction du temps t est donnée par :
La représentation de la tension aux bornes du condensateur en
fonction du temps est donnée ci-dessous. 1.
En considérant l’expression de la tension
uC d’une part, et la représentation graphique d’autre
part, déterminer la force électromotrice E de la pile. 2.
Déterminer graphiquement le temps
caractéristique τ de la charge de ce dipôle. 3.
En déduire la résistance interne r de
la pile. |
|
Caractéristiques d’une pile :
-
Graphe : 1.
Force électromotrice E de la pile.
-
Schéma du montage :
- On considère la pile comme l’association série d’une source idéale de tension de force électromotrice E et d’une résistance r (résistance
interne de la pile).
-
Loi des mailles avec l’orientation
choisie :
-
E =
ur +
uC
-
ur =
r .
i et
-
Équation différentielle vérifiée par
uC :
-
-
La solution est bien du type :
-
avec
τ =
r . C
-
Lorsque
t → ∞,
-
-
Pour connaître la valeur de la force
électromotrice de la pile, on trace l’asymptote horizontale à la
courbe uC =
f (t) lorsque
t → ∞.
-
La valeur de l’ordonnée donne la
force électromotrice E de
la pile.
-
Lecture graphique :
E ≈ 8,8 V 2.
Temps caractéristique τ de la charge
de ce dipôle.
-
La durée de charge du condensateur
d'un dipôle (R, C)
dépend de la résistance R
du conducteur ohmique et de la capacité
C du
condensateur.
-
τ =
R .
C.
-
Dans le cas présent :
-
-
Pour déterminer graphiquement la
valeur de τ, on trace la tangente à l’origine à la courbe
uC = f (t).
-
L’abscisse du point
M d’intersection de la tangente avec l’asymptote horizontale donne
la valeur de la constante de temps
τ.
-
À partir du graphe : τ ≈ 0,70
ms
-
On peut utiliser le fait qu’au temps
t =
τ,
-
uC (τ)
= 0,63 E.
-
les deux méthodes donnent la même
valeur : τ ≈ 0,70 ms 3.
Résistance interne r de la pile.
-
On peut déterminer la valeur de la
résistance interne r de
la plie à partir de la connaissance de la valeur du temps
caractéristique τ.
-
|
||||||||
11)- Exercice 22 page 439 : Le défibrillateur :
|
Le défibrillateur : A.
Défibrillateur cardiaque. Un défibrillateur cardiaque permet d’appliquer un choc électrique sur le thorax d’un patient, dont les fibres musculaires du cœur se contractent de façon
désordonnée (fibrillation). B.
Schéma simplifié du circuit électrique d’un
défibrillateur cardiaque :
-
Schéma :
Avant d’appliquer le choc électrique au patient, la source de tension charge le condensateur. Le graphique ci-dessous représente la tension uC
aux bornes du condensateur au cours de cette charge en fonction du temps t. 1.
Montrer que l’équation différentielle
vérifiée par la tension aux bornes du condensateur peut s’écrire :
2.
Montrer que la solution de cette équation
différentielle est
3.
Déterminer le temps caractéristique de cette
charge. 4.
En
déduire la résistance interne r de la source de
tension. 5. Le thorax du patient est assimilé à un conducteur ohmique de résistance R = 50 Ω. Calculer l’intensité du courant
circulant dans le thorax eu début de la décharge. |
|
Le défibrillateur : 1.
Équation différentielle vérifiée par la
tension aux bornes du condensateur:
-
Schéma du montage :
-
La loi des mailles :
-
E =
uC +
ur
-
Avec l’orientation choisie :
-
ur =
r .
i et
-
On en déduit l’équation
différentielle vérifiée par la tension
uC aux bornes
du condensateur.
-
-
Cette relation est bien en accord
avec celle donnée dans l’énoncé.
-
2.
Solution de cette équation différentielle.
-
-
L’équation différentielle vérifiée
par la tension uC lors de la charge est du type :
-
y’ =
a .
y + b avec
a ≠ 0,
-
Elle admet des solutions du type :
-
-
La constante
K est liée aux conditions initiales.
-
Les constantes
a et b sont liées aux
caractéristiques du circuit.
-
En utilisant la formulation
précédente :
-
-
Avec comme solution :
-
-
On en déduit que :
-
-
Recherche de l’expression de
K :
-
Au temps
t = 0 s,
uC (0) = 0 le
condensateur est déchargé :
-
-
De plus la constante de temps du
circuit est donnée par la relation :
-
τ =
r ×
C
-
On en déduit la relation suivante :
-
-
-
Exploitation graphique :
-
Valeur de
E :
-
Lorsque
t → ∞,
-
-
Pour connaître la valeur de
E, on trace l’asymptote horizontale à la courbe
uC =
f (t) lorsque
t → ∞.
-
La valeur de l’ordonnée donne la
valeur E. 3.
Temps caractéristique de cette charge.
-
τ =
r ×
C.
-
Dans le cas présent :
-
-
Pour déterminer graphiquement la
valeur de τ, on trace la tangente à l’origine à la courbe
uC = f (t).
-
L’abscisse du point
M d’intersection de la tangente avec l’asymptote horizontale donne
la valeur de la constante de temps
τ.
-
À partir du graphe : τ ≈ 0,48
s
-
On peut utiliser le fait qu’au temps
t =
τ,
-
uC (τ)
= 0,63 E.
-
Les deux méthodes donnent la même
valeur : τ ≈ 0,48 s 4.
Résistance
interne r de la source de tension.
-
On peut déterminer la valeur de la
résistance interne r de
la plie à partir de la connaissance de la valeur du temps
caractéristique τ.
-
5.
Intensité du courant circulant dans le
thorax eu début de la décharge.
-
Le thorax du patient est assimilé à
un conducteur ohmique de résistance :
-
R
= 50 Ω
-
Au temps
t = 0 s, le condensateur
est chargé et uC
(0) ≈ 1,5 ×103 V
-
On ferme l’interrupteur :
-
Schéma équivalent avec l’orientation
pour i dans le circuit :
-
Loi des mailles :
-
uC +
uR = 0
-
Avec l’orientation choisie :
-
uR =
R .
i et
-
On en déduit l’équation
différentielle vérifiée par la tension
uC aux bornes
du condensateur.
-
-
On en déduit l’équation
différentielle vérifiée par la tension uC lors de
la décharge :
-
-
Les solutions d’une équation
différentielle y’ = a . y + b avec a
≠ 0, sont de la forme :
-
-
La constante K est liée aux
conditions initiales.
-
Les constantes a et b
sont liées aux caractéristiques du circuit.
-
En utilisant la formulation
précédente :
-
-
Avec comme solution :
-
-
On en déduit que :
-
-
Recherche de l’expression de K :
-
Au temps t = 0 s, uC
(0) = E : le
condensateur est chargé :
-
K = E
-
Solution de l’équation
différentielle :
-
►
Expression de l’intensité du courant
lors de la décharge du condensateur :
-
-
-
-
On remarque que lors de la décharge,
le courant i circule dans
le sens opposé à celui choisi lors de l’orientation du circuit.
-
Au temps
t = 0, l’intensité dans
le circuit est maximale en valeur absolue.
-
-
À l’instant initial, l’intensité du
courant, en valeur absolue, est voisine de 30 A. |
||||||||
12)- Exercice 27 page 441 : Capteur capacitif de pression :
|
Capteur capacitif de pression : Les capteurs capacitifs de pression sont utilisés dans de
nombreux dispositifs industriels visant à déterminer, par exemple, le taux de remplissage d’une cuve fermée
hermétiquement. A.
Capteur capacitif de pression relative. Un capteur capacitif de pression relative est constitué de deux armatures métalliques, l’une fixe et rigide, l’autre souple, placées face à face. Ce capteur capacitif permet
de mesurer une pression relative ΔP par rapport à la pression atmosphérique Patm : ΔP = P – Patm : Schémas :
B.
Capacité d’un condensateur plan. La capacité C (en F) d’un condensateur plan de surface
S (en m2) et dont le diélectrique, d’épaisseur e
(en m), est constitué d’air, est donnée par la relation suivante :
1.
Quelle est la pression relative mesurée par
le capteur capacitif lorsque la pression P est égale à la
pression atmosphérique ? 2.
Ce capteur peut-il être assimilé à un
condensateur plan ? 3.
Comment la capacité de ce capteur
évolue-t-elle lorsque la pression augmente du côté de l’armature
souple ? 4.
Le capteur présenté est caractérisé par des
armatures de diamètre D = 10 cm et d’épaisseur e = 1,0
mm. a.
Calculer la capacité C de ce capteur. b.
Son ordre de grandeur est-il usuel ?
|
|
Capteur capacitif de pression :
-
1.
Pression relative mesurée par le capteur
capacitif lorsque la pression P est égale à la pression
atmosphérique :
-
Ce capteur capacitif permet de
mesurer une pression relative ΔP par rapport à la pression
atmosphérique Patm :
-
ΔP =
P –
Patm
-
Si
P =
Patm
-
Alors :
ΔP = 0
-
La pression relative mesurée est
nulle. 2.
Capteur capacitif et condensateur plan :
-
Schéma :
-
Le dispositif est constitué de deux
armatures métalliques séparées par un diélectrique, l’air.
-
On est bien en présence d’un
condensateur plan.
-
Vue de profil :
3.
Évolution de la capacité :
-
Lorsque la pression augmente du côté
de l’armature souple, l’armature souple se déforme légèrement et
l’épaisseur e diminue.
-
Comme pour le condensateur plan :
-
La capacité du condensateur est
proportionnelle à la surface
S des armatures en regard.
-
La capacité d’un condensateur plan
est inversement proportionnelle à son épaisseur
e.
-
Si l’épaisseur
e ⸔ diminue, la capacité
du condensateur C
⸕ augmente. 4.
Capaciré du condensateur plan : a.
Capacité C de ce capteur.
-
Armatures de diamètre :
-
D = 10 cm
-
Épaisseur :
-
e = 1,0 mm
-
b.
Ordre de grandeur de la capacité :
-
L’ordre de grandeur est de la
centaine de picofarad.
-
C’est une grandeur usuelle. |
|
|