QCM réalisé avec le logiciel Questy

Pour s’auto-évaluer

AIDE

Interactions, Forces et Champs

L’attraction gravitationnelle :

-  On parle aussi d’attraction gravitationnelle.

-  Loi de Newton : 1687

-  Énoncé :

-  Deux corps ponctuels A et B, de masses m_A et m_B, séparés par une distance r, exercent l’un sur l’autre des forces attractives.

-  Le corps A exerce sur le corps B la force

-   

-  Le corps B exerce sur le corps A la force

-   

-  Ces deux forces ont : même direction :

-  La droite (AB), même valeur et des sens opposés.

-  Expression de la valeur :

-   

-  Expression vectorielle :

-   

-   

-  Conséquence :

-   

-  G est appelé la constante de gravitation universelle :

-  G ≈ 6,67 × 10^–11 m³ . kg^–1 . s^–2 ou m² . kg^–2 . N

-  Unités :

-  La force F s’exprime en newton (N) et les masses en kilogramme (kg).

-  Valeur des masses m et m’ en kg.

-  Distance séparant les deux masses ponctuelles : r en m

-  Schéma :

-  Autre expression (en utilisant le vecteur unitaire ) :

-   

-   

Attraction gravitationnelle et distance entre les deux corps :

-   

-  Les forces de gravitation, sont :

-  Proportionnelles aux grandeurs qui les créent (les masses)

-  Et inversement proportionnelle au carré de la distance (qui les séparent)

-  La valeur de la force est inversement proportionnelle au carré de la distance r.

-  Si r’ = 2 r => (r’)² = 4 (r)²

-  Si la distance entre les deux corps en interaction gravitationnelle double, la norme de la force est divisée par quatre.

Attraction gravitationnelle et la masse de chaque corps :

-  Les forces de gravitation, sont :

-  Proportionnelles aux grandeurs qui les créent (les masses)

-  Si m’_A = 2 m_A et m’_B = 2 m_B alors m’_A . m’_B = 4 m_A . m_B

-  F’_A/B = F’_B/A = 4 F_A/B = 4 F_B/A

-  Si la masse de chaque corps en interaction gravitationnelle est multipliée par deux, la norme de la force est multipliée par quatre.

Norme des forces gravitationnelles :

-  Les forces de gravitation, sont :

-  Proportionnelles aux grandeurs qui les créent (les masses)

-  Et inversement proportionnelle au carré de la distance (qui les séparent)

Champ de gravitation :

-  Valeur du champ créé par la masse m_A située au point O de l’espace  :

-   

-  Le champ de gravitation créé par un astre de masse m est proportionnel à sa masse m et inversement proportionnel au carré la distance d.

-  Ce résultat se généralise à des corps à répartition sphérique de masse (comme les astres).

-  La masse est répartie de façon régulière autour du centre du corps.

-  C’est le cas de la Terre, de la Lune, des planètes et des étoiles.

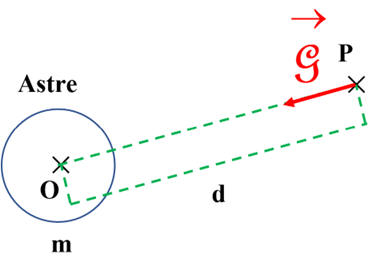
Le champ gravitationnel :

-   

-  Le champ est radial et orienté vers la source de champ, dans le cas présent l’astre.

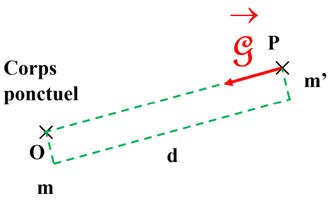
Champ gravitationnel créé par un corps ponctuel de masse m situé au point O de l’espace :

-  Schéma :

-   

-  Le champ de gravitation créé par un corps ponctuel de masse m est proportionnel à sa masse m et inversement proportionnel au carré la distance d (distance OP).

-  Le champ est radial et orienté vers la source de champ, dans le cas présent le corps ponctuel de masse m situé au point O de l’espace.

-  Dans le cas présent, la masse m située au point O de l’espace constitue la source de champ .

Le vecteur vitesse :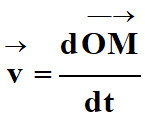

-  Caractéristiques du vecteur vitesse.

-  Origine : position occupée par le point mobile à l'instant considéré t.

-  Direction : tangente à la trajectoire au point considéré.

-  Sens : celui du mouvement à cet instant.

-  Valeur : celle de la vitesse instantanée à cet instant.

-  Définition :

-  Dans un référentiel R donné, le vecteur vitesse , d’un point M à l’instant t, est égal à la dérivée, par rapport au temps, du vecteur position  à cet instant

►  Représentation du vecteur vitesse.

-  Le vecteur vitesse est tangent à la trajectoire au point considéré.

Le vecteur accélération :

-  Dans un référentiel R donné, le vecteur accélération d’un point M à l’instant t, est égal à la dérivée , par rapport au temps, du vecteur vitesse  à cet instant :

-  Le vecteur accélération traduit les variations du vecteur vitesse.

Chap N° 11

Mouvement et

deuxième loi de Newton

Repère de Frenet :

-  Ce repère est bien utile pour l’étude des mouvements circulaires (uniformes)

-  Considérons un point mobile M animé d’un mouvement circulaire uniforme.

-  La trajectoire est un cercle de centre O et de rayon R et la valeur de la vitesse ne change pas au cours du temps.

-  Pour simplifier l’étude d’un tel mouvement et en déduire les caractéristiques, il faut utiliser le repère de Frenet :

-   

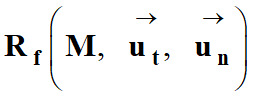
-  : désigne un vecteur unitaire tangent à la trajectoire et orienté dans le sens du mouvement.

-  : désigne un vecteur unitaire perpendiculaire à et orienté vers le centre O du cercle.

-  Le vecteur vitesse est tangent à la trajectoire au point considéré .

-  Le vecteur vitesse change de direction à chaque instant.

-  Pour obtenir les coordonnées du vecteur accélération, il faut dériver cette expression par rapport au temps.

-  (1) ceci se dérive comme un produit.

-  Le vecteur accélération peut se décomposer de la façon suivante :

-   

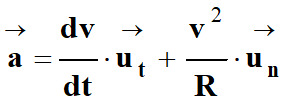
-  En conséquence, le vecteur accélération peut être décomposé en une :

-  Accélération tangentielle  qui dépend de la variation de la valeur de la vitesse :

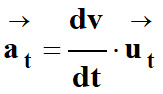-  avec

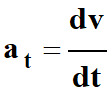
-  Accélération normale  qui est liée à la variation de la direction du vecteur vitesse.

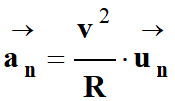-  avec

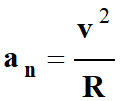
-  Autre expression du vecteur accélération :

-   

Cas d’un mouvement circulaire uniforme :

-  Caractéristiques du vecteur vitesse et du vecteur accélération : 

-  Le vecteur vitesse est à chaque instant perpendiculaire au vecteur accélération.

-  Le vecteur vitesse et le vecteur accélération changent de direction à chaque instant.

-  L’accélération est centripète.

Vidéo

Mouvement circulaire uniforme et vecteur accélération :

-  Le vecteur accélération  comprend :

-  Accélération tangentielle  qui dépend de la variation de la valeur de la vitesse :

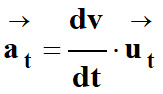-  avec

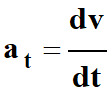
-  Comme v = cte => a_t = 0

-  Accélération normale qui est liée à la variation de la direction du vecteur vitesse.

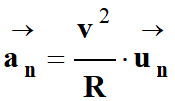-  avec

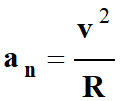
-  En conséquence :

-   

-  L’accélération et centripète.

-  Elle change de direction à chaque instant.

-  Sa norme est constante et le vecteur accélération  varie.

Deuxième loi de Newton :

-   

-  Comme m > 0, le vecteur accélération et le vecteur somme vectorielle des forces appliquées au système ont même direction et même sens.

Deuxième loi de Newton et système soumis à une force de norme constante non nulle :

-  La valeur de la force F = cte ≠ 0, mais le vecteur force  peut changer de direction.

-   

-  D’après cette relation  et  ont même direction et même sens à chaque instant.

-   

-  Si F = cte ≠ 0 alors a_G = cte ≠ 0

-  Le mouvement ne peut pas être rectiligne uniforme car dans ce cas a_G = 0.

Deuxième loi de Newton, vecteur accélération et somme vectorielle des forces :

-   

-   

-  Si   =>

-  Comme m > 0, le vecteur accélération et le vecteur somme vectorielle des forces appliquées au système ont même direction et même sens.

-  Si  change de sens,  alors  change de sens.

-  Si m’ = 2 m et

-
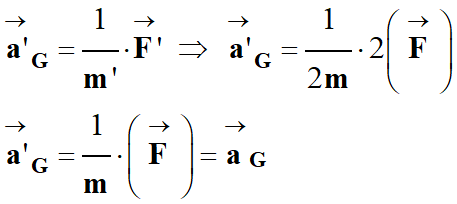