I- Émission et propagation d’un signal sonore.

1)- Émission d’un signal sonore.

-  Mis en vibration, un objet émet un signal sonore.

-  Pour que ce signal sonore soit  audible, il faut l’amplifier.

-  Pour ce faire, on utilise le plus souvent une caisse de résonance.

-  Exemple : la contrebasse

-  Lorsque l’on fait vibrer les cordes d’une contrebasse, celles-ci produisent un son.

-  Ce son est alors amplifié par le corps de la contrebasse qui fait office de caisse de résonance.

2)- Propagation d’un signal sonore.

-  Son émis par un haut-parleur :

-  Lorsqu’un haut-parleur est soumis à une tension périodique, sa membrane vibre.

-  Cela crée une vibration de l’air qui se propage de proche en proche sans transfert de matière : c’est une onde sonore.

-  Schéma d’un haut-parleur :

Vidéo

-  Propagation d’un son :

Vidéo

-  Les molécules qui constituent l’air vibrent et transmettent ce mouvement de proche en proche aux molécules voisines.

-  Quelques points importants :

-  Un signal sonore a besoin d’un milieu matériel pour se propager.

  Un signal sonore se propage dans un milieu matériel solide, liquide ou gazeux mais ne se propage pas dans le vide.

-  Les vitesses de propagation d’un signal sonore dépendent du milieu matériel de propagation.

-  On parle aussi de la célérité d’un son.

-  La valeur approchée de la vitesse de propagation d’un signal sonore dans l’air à environ 20 ° C est :

-  v  ≈  340 m / s.

-  cette vitesse dépend de la température.

-  La célérité du son dépend du milieu de propagation.

-  La célérité du son est plus grande dans les solides que dans les liquides et le gaz.

-  Car moins le milieu est compressible, plus il est difficile à déformer et plus il est rigide.

-  Plus il est rigide, plus grande est sa célérité.

-  Tableau de comparaison :

-  Comparaison de cette valeur avec d’autres valeurs de vitesse.

3)- Caractéristiques d’un signal sonore périodique.

a)-   Définition :

Un phénomène périodique est un phénomène qui se reproduit identique à lui-même à intervalles de temps réguliers.

-  Exemple :

-  Signal émis lors de la réalisation d’un audiogramme :

b)-  Période et fréquence :

-  La période T d’un phénomène périodique est la durée au bout de laquelle le phénomène se reproduit identique à lui-même.

-  L’unité de période T est la seconde, symbole s.

-  La fréquence f représente le nombre de période par seconde. On écrit :

-   

-  unité de fréquence : Hertz : symbole  Hz

-  Remarque : Pour obtenir la fréquence en Hz, il faut pour cela exprimer la période en seconde s.

c)-   Enregistrement d’un signal sonore

-  C’est la représentation temporelle du signal électrique, de la tension u = f (t), obtenue à l’aide d’un microphone.

-  Exemple :

-  L’analyse du signal délivré par un microphone qui capte cette onde sonore montre que les vibrations captées par le récepteur ont la même fréquence f  que celle de la tension périodique appliquée aux bornes du H.P.

-  L’analyse du signal délivré par le GBF et du signal reçu par le microphone montre que les vibrations captées par le récepteur ont la même fréquence f que celle de la tension périodique.

d)-  Tension maximale, tension minimale : Amplitude

-  Pour une tension périodique u (t), la tension maximale U_max désigne la valeur la plus élevée prise par u (t) au cours du temps.

-  La tension minimale U_min est sa valeur la plus faible.

-  L’amplitude de la tension représente l’écart entre sa valeur maximale et sa valeur moyenne.

-  Application :

-  Déterminer, pour le signal suivant :

-  les valeurs de U_max et U_min

-  La valeur de l’amplitude A:

-  Sa période T et sa fréquence f.

-  U_max ≈ 50 mV et  U_min ≈ - 50 mV

-  Remarque : U_max = – U_min la tension est dite symétrique.

-  Comme la tension est symétrique, la valeur moyenne est nulle pour cette tension.

-  A = U_max ≈ 50 mV

-  C’est un cas particulier fréquent.

-  On peut déterminer aussi la valeur de la période T et ainsi la valeur de la fréquence f.

-  Période du signal :

-  5 T ≈ 2,0 ms  => T ≈ 0,40 ms

-  Fréquence du signal :

-   

II- La perception d’un son.

1)- Domaines de fréquences.

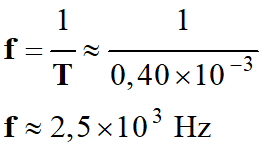
-  L’oreille humaine est un récepteur sensible aux ondes sonores dont la fréquence est comprise entre 20 Hz et 20 kHz.

-  Domaines des ondes sonores :

2)- Hauteur et timbre.

-  Les sons émis par deux cordes différentes d’une guitare n’ont pas la même fréquence.

-  Ils n’ont pas la même hauteur.

-  Plus la hauteur d’un son est grande, plus sa fréquence est élevée et plus le son est aigu.

-  D’autre part, plus un son est grave et plus sa fréquence est basse.

-  Le timbre d’un son dépend du nombre et de l’amplitude des harmoniques qui sont présents.

-  Deux sons de même hauteur émis par des instruments différents ne sont pas perçus de la même manière, car les harmoniques, associées au fondamental, sont différentes.

-  L’analyse spectrale d’un son musical permet de caractériser :

-  La hauteur du son qui est liée à la fréquence f₁ du fondamental

-  Le timbre du son qui est lié au nombre et à l’amplitude des harmoniques présentes.

-  Le timbre du son émis dépend de l'instrument de musique mais aussi du point d'attaque.

3)- Intensité et niveau d’intensité sonore.

-  Le niveau d’intensité sonore est lié à l’amplitude du signal sonore.

-  Plus l’amplitude du signal sonore est élevée plus l’intensité sonore I est grande.

-  L’intensité sonore, notée I, caractérise l’intensité du signal reçue par l’oreille.

-  Elle s’exprime en watt par mètre carré : W / m² ou W. m^–2

-  L’oreille humaine normale perçoit les signaux sonores dont l’intensité est comprise entre

-  Une valeur minimale I₀ = 1,0 × 10^–12 W. m^–2 (seuil d’audibilité)

-  Et une valeur maximale I_max = 25 W. m^–2 (seuil de douleur).

-  Comme l’écart entre ces deux valeurs est très grand, on a créé une nouvelle grandeur, qui utilise une échelle logarithmique :

-  Appelée le niveau d’intensité sonore, notée L.

-  Le niveau d’intensité sonore L s’exprime en décibel dB

-  L’intensité sonore I et le niveau d’intensité sonore L varient dans le même sens.

-  Quand I augmente, L augmente.

-  Le niveau d’intensité sonore se mesure avec un sonomètre.

-  Remarque : l’intensité sonore I n’est pas proportionnelle au niveau d’intensité sonore L.

-  Échelles de I et L :

-  Remarque : les valeurs de L (dB) sont plus faciles à manipuler que les valeurs de I (W. m^–2)

4)- L’exposition sonore.

-  Plus le niveau d’intensité sonore et la durée d’exposition sont élevés et plus les risques d’atteinte de l’audition sont importants.

-  Remarque :

-  Lorsque plusieurs instruments de musique jouent ensemble, les intensités sonores I dues à chaque instrument s’ajoutent, alors que les niveaux d’intensité sonore L ne s’ajoutent pas.

-  L’exposition sonore tient compte du niveau d’intensité sonore et de la durée d’exposition auxquels l’oreille est soumise.

-  Une exposition sonore trop élevée peut avoir des conséquences irréversibles, comme une surdité partielle, voire totale.

-  Une exposition sonore de quelques secondes à un niveau d’intensité sonore L supérieur à 120 dB peut entraîner une surdité totale et c’est irréversible.

III- Applications :

1)- Représentation temporelle d’un signal périodique.

-  Un microphone permet de convertir un signal sonore en un signal électrique.

-  Cette tension a la même période que le signal sonore.

-  L’analyse de la représentation temporelle du signal électrique permet d’étudier le signal sonore.

-  Trois signaux sonores sont émis. Ils ont pour fréquence

a.   f₁ = 8,0 × 10² Hz

b.   f₂ = 4,0 × 10² Hz

c.   f₃ = 2,0 × 10² Hz

-  Les signaux électriques obtenus lors de l’acquisition de ces trois signaux sonores sont représentés ci-dessous.

-  Exploiter chaque signal pour déterminer la valeur de la période et en déduire la valeur de la fréquence sur l’oscillogramme.

-  Faire attention aux réglages.

 Réponses :

-  Étude de l’enregistrement a.

-  Valeur de la période du signal : exploitation de l’oscillogramme :

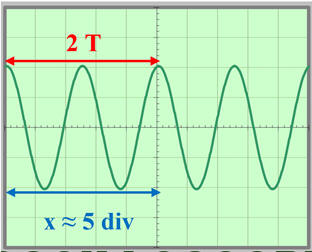
-  Durée de balayage :

►    Durée de balayage : b = 0,50 ms / div

-  Pour deux périodes, x ≈ 5 div

-  2 T =  x . b

-  2 T ≈ 2,5 × 0,50

-  T ≈ 1,25 ms

-  On en déduit la fréquence du signal :

-   

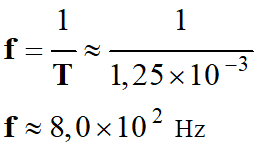
-  Ce résultat est en accord avec la valeur du signal a. avec f₁ = 8,0 × 10² Hz

-  Étude de l’enregistrement b.

-  Valeur de la période du signal : exploitation de l’oscillogramme :

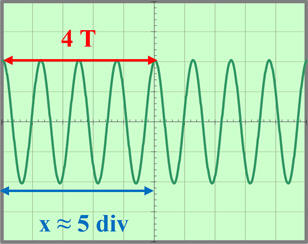
-  Durée de balayage :

►    Durée de balayage : b = 2 ,0 ms / div

-  Pour quatre périodes, x ≈ 5 div

-  4 T =  x . b

-  4 T ≈ 5,0 × 2,0

-  T ≈ 2,5 ms

-  On en déduit la fréquence du signal :

-   

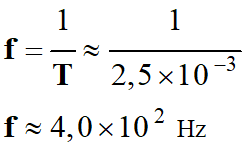
-  Ce résultat est en accord avec la valeur du signal b. avec f₂ = 4,0 × 10² Hz

-  Étude de l’enregistrement c.

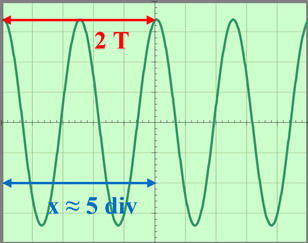
-  Valeur de la période du signal : Exploitation de l’oscillogramme :

-  Durée de balayage :

►    Durée de balayage : b = 2 ,0 ms / div

-  Pour deux périodes, x ≈ 5 div

-  2 T =  x . b

-  2 T ≈ 5,0 × 2,0

-  T ≈ 5,0 ms

-  On en déduit la fréquence du signal :

-   

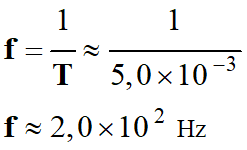
-  Ce résultat est en accord avec la valeur du signal c. avec f₃ = 2,0 × 10² Hz

2)- QCM.

L'émission et la propagation d'un signal sonore.

La perception d'un son.

QCM réalisé avec le logiciel QUESTY

pour s'auto-évaluer

Sous forme de tableau

3)- Exercices.