I- Introduction et rappels.

1)- Modélisation d’une lentille mince convergente.

a)-  Représentation symbolique d’une lentille mince convergente.

-  Une lentille mince est caractérisée par trois points particuliers :

-  Son centre optique O ;

-  Son foyer image F’ ;

-  Son foyer objet F.

-  Représentation symbolique :

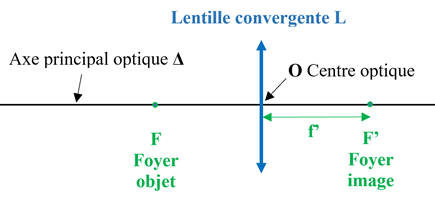
-  La distance focale d’une lentille convergente :

-  La distance focale f' est définie comme la distance entre le centre optique O et chacun des foyers F et F’.

-  On la note f' :

-  C'est une grandeur positive pour une lentille convergente.

-  Le foyer objet F et le foyer image F’ sont symétriques par rapport au centre optique O.

-   f’ = OF’ = OF

- 

-  La loi du retour inverse de la lumière permet de dire que tout rayon passant par F, symétrique de F’ par rapport au centre optique O émerge parallèlement à l’axe optique Δ.

b)-  Construction d’une image réelle :

-  Application :

-  Données : Diamètre de la lentille : 6,0 cm

-  Distance focale : f’ = 2,0 cm

-  L’objet est perpendiculaire à l’axe optique.

-  Objet AB = 1,0 cm

-  L’objet AB est situé avant le foyer-objet à 1,5 cm du foyer-objet.

-  Réaliser la construction en utilisant la méthode suivante :

-  Rayon 1 : issu du point B et passant par le centre optique : il n’est pas dévié.

-  Rayon 2 : issu du point B et parallèle à l’axe optique. Il émerge de la lentille en passant par le point F’ foyer - image.

-  Rayon 3 : issu du point B et passant par F (foyer - objet). Il émerge de la lentille parallèlement à l’axe optique.

-  Les mesures :

-  f’ = 2,0 cm

-  AF = 1,5 cm

-  AB = 1,0 cm

-  A’B’ ≈ 1,3 cm

-  Remarques :

-  Les trois rayons se coupent en B’ image de B.

-  L’image A’ de A est la projection orthogonale de B’ sur l’axe principal.

-  L’objet AB est réel et l’image A’B’ est réelle et renversée.

-  Dans le cas présenté, l’image est plus grande que l’objet.

-  La construction de l’image A’B’ permet de déterminer graphiquement sa position, sa taille et son sens.

2)- Repère associé à un lentille mince convergente.

-  On choisit un repère R (O, x, y)

-  L’origine est le point O, centre optique de la lentille.

-  L’axe des abscisses x est l’axe optique Δ de la lentille. Il est orienté dans le sens de propagation de la lumière.

-  L’axe des ordonnées y est l’axe perpendiculaire à l’axe optique Δ, passant par le centre optique O de la lentille. Il est orienté vers le haut.

-  Ainsi,

-  La position de l’objet AB et celle de l’image A’B’ sont respectivement repérées par les abscisses x_A de A et x_A’ de A’.

-  Schéma :

Repérage de la position de l’objet et de son image

II- Les relations de conjugaison et de grandissement.

1)- Position et taille de l’image.

a)-  Approche de la relation.

-  La position de l’image est liée à la position de l’objet par rapport à la lentille et à la distance focale de la lentille.

-  Il est possible, par le calcul, de prévoir le résultat de la construction géométrique de l’image.

-  Pour cela, on utilise le repère R (0, x, y) associé à la lentille mince convergente.

-  La position de l’objet AB et celle de l’image A’B’ sont respectivement repérées par les abscisses x_A de A et x_A’ de A’.

-  Les abscisses x_A et x_A’, la distance focale f’ de la lentille, ne sont pas indépendantes.

-  Elles sont reliées par une relation appelée : relation de conjugaison.

b)-  Relation de conjugaison :

-  Formule de conjugaison avec les notations choisies :

-   

-  Remarque :

-  Les grandeurs x_A, x_A’ et f’ doivent être exprimées dans la même unité de longueur.

c)-  Relation de conjugaison et formule de Descartes :

-  Cette relation fait intervenir les mesures algébriques :

-  Formule de conjugaison  avec les mesures algébriques :

-   

-  Formule de Descartes :

-  

-  Formule de conjugaison qui fait intervenir les coordonnées liées au repère associé à la lentille :

-   

-  Schéma de la situation :

-  Retrouver cette relation en utilisant le fait que les triangles OBA et OB’A’ d’une part et HOF’ et B’A’F’ d’autre part sont homothétiques (Théorème de Thalès).

Et

-  Remarque : H est la projection orthogonale de B sur la lentille.

-  Les triangles OBA et OB’A’ sont homothétiques, d’après Thalès :

-  (1)

-  Les triangles HOF’ et B’A’F’ sont homothétiques, d’après Thalès :

-   

-  En combinant (1), (2) et (3), il vient :

-   

-  En utilisant le fait que :

-   

-  En identifiant les différents termes de la relation :

- 

d)-  Grandissement de l’image :

-  Le grandissement d’une lentille est donné par la relation :

-   

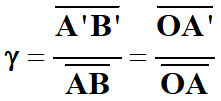
-  Avec le repère lié à la lentille mince convergente :

-  et

-  Le grandissement de l’image est donné par la relation suivante :

-   

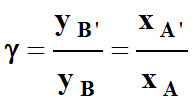
-  Remarques :

-  La grandeur γ est un nombre qui n’a pas d’unité.

-  C’est une grandeur algébrique : elle peut être positive ou négative.

-  Si γ  >  0 l’image a le même sens que l’objet, on dit qu’elle est droite.

-  Si γ <  0  l’image est de sens contraire à l’objet, on dit qu’elle est renversée.

-  Si | γ | >1, l’image est plus grande que l’objet.

-  Si| γ | <1 , l’image est plus petite que l’objet.

e)-  Conclusion :

-  La position, la taille et le sens de l’image sont les caractéristiques de l’image.

-  Elles peuvent être déterminées graphiquement ou par le calcul à partir des relations de conjugaison et du grandissement.

-  Les caractéristiques de l’images dépendent des caractéristiques de la lentille et des caractéristiques de l’objet.

f)-  Comment déterminer la valeur de la distance focale f’ d’une lentille mince convergente ?

-  Soit f’ la distance focale d’une lentille mince convergente.

-  La relation de conjugaison est la suivante.

-   

-  Si on vise un objet AB suffisamment éloigné de la lentille,

-  Le terme x_A devient très grand et le terme tend vers zéro

-  En conséquence,

-   

-  La distance entre la lentille et l’image est pratiquement égale à la distance focale de la lentille.

-  Image du Soleil donné par une lentille mince convergente :

-  Une lentille, dont l’axe optique est dirigé vers le Soleil, donne sur un écran une tache quasi ponctuelle très lumineuse.

-  Cette tache représente l’image du Soleil (Attention ça chauffe).

-  On peut considérer que le Soleil est une source lumineuse située à l’infini.

-   

-  La distance entre la lentille et l’image est pratiquement égale à la distance focale de la lentille.

-  On a ainsi une idée de l’ordre de grandeur de la distance focale de la lentille.

2)- Mise au point.

-  Pour que l’image d’un objet se forme sur la rétine d’un œil ou sur le capteur d’un appareil photographique, il faut réaliser une mise au point.

-  Pour ce faire, on peut :

-  Modifier la distance focale de la lentille,

-  Modifier la distance de l’objet à la lentille,

-  Modifier la distance de la lentille à l’écran.

III- Le lien entre la position de l’objet et les caractéristiques de l’image.

1)- Premier cas : l’objet AB est situé avant le foyer objet F.

a)-  Schéma de la situation :

b)-  Caractéristiques de l’image.

-  L’image formée à travers la lentille peut être observée sur un écran

-  On dit que l’image est réelle : x_A’ > 0

-  Le grandissement γ <  0 : l’image est renversée.

-  | γ | <  1 , l’image est plus petite que l’objet.

2)- Deuxième cas : L’objet AB est situé en le foyer objet F et le centre optique O.

a)-  Schéma de la situation :

b)-  Caractéristiques de l’image.

-  L’image formée à travers la lentille ne peut pas être observée sur un écran.

-  Ce sont les prolongements des rayons 1, 2 et 3 qui se coupent en B’

-  L’image est virtuelle.

-  Elle ne se forme pas sur un écran mais elle peut être vue par l’œil à travers le système optique.

-  Il faut placer l’œil sur le chemin des rayons lumineux qui émergent du système optique.

-  Le grandissement γ >  0 : elle est dite droite.

-  L’image est de même sens que l’objet :.

-  | γ | >  1 , l’image est plus grande que l’objet.

c)-  Application : La loupe.

-  À l’aide d’une loupe constituée par une lentille convergente de distance focale f’ = 5,0 cm, un philatéliste observe les détails d’un timbre et, en particulier une lettre de 0,10 mm de hauteur.

-  La lettre jouant le rôle d’objet AB est placée au foyer objet F de la lentille.

-  L’œil de l’observateur, assimilable à un point, est placé au foyer image F’ de la lentille.

Questions :

-  L’image A’B’ est-elle à l’infini ou à une distance finie de la lentille ?

Construction :

-  Tracer la marche de deux rayons issus du point B, l’un parallèle à l’axe optique et l’autre passant par le centre optique.

-  Tracer la marche d’un faisceau s’appuyant sur les bords de la lentille.

-  Tracer la marche du rayon lumineux issu de B’ et pénétrant dans l’œil de l’observateur.

-  On place un objet AB de 1,0 cm de haut à 4,0 cm du centre optique.

-  Le point A est sur l’axe optique et AB est perpendiculaire à l’axe optique.

-  Construire l’image A’B’ de AB donnée par la loupe ceci à l’échelle ½ pour la lentille mais pas pour l’objet.

-  Déterminer graphiquement la position et la grandeur de l’image.

-  En déduire le grandissement de la loupe dans cette situation.

-  Donner les caractéristiques de l’image.

-  Retrouver les grandeurs x_A et x_A’ et y_B et y_B’ à l’aide des formules de conjugaison.

-  Peut-on recueillir cette image sur un écran  ?

Réponses :

-  Position de l’image A’B’ :

-   Comme l’objet est placé au foyer objet de la lentille convergente, l’image est située à l’infinie.

-  Schéma :

-  Le rayon 1 et le rayon 2 sont parallèles.

-  Construction :

-  Le tracé des deux rayons issus du point B, l’un parallèle à l’axe optique et l’autre passant par le centre optique :

-  Le tracé de la marche d’un faisceau s’appuyant sur les bords de la lentille.

-  Le tracé de la marche du rayon lumineux issu de B’ et pénétrant dans l’œil de l’observateur.

-  Construction de l’image A’B’ de AB donnée par la loupe ceci à l’échelle ½ pour la lentille mais pas pour l’objet.

-  Détermination graphique de la position et de la grandeur de l’image :

-  Position de l’image :

-  x_A’ ≈ – 20 cm  et y_B’ ≈  5,0 cm 

-  Taille de l’image : A’B’ ≈ 5,0 cm

-  Le grandissement de l’image est donné par la relation suivante :

- 

-  Caractéristiques de l’image :

-  L’image est virtuelle.

-  Le grandissement γ >  0 : elle est dite droite.

-  | γ | >  1 , l’image est plus grande que l’objet.

-  Les grandeurs x_A et x_A’ et y_B et y_B’

-  La formule de conjugaison :

-   

-  Grandissement de l’image :

-   

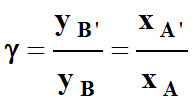
-  Données initiales :

-  f’ = 5,0 cm ; x_A = – 4,0 cm ; y_B = 1,0 cm

-  Schéma de la situation :

-  Comme l’objet est situé entre le foyer objet et le centre optique, l’image se trouve à gauche de la lentille.

-  Valeur de x_A’ :

-   

-  Valeur de y_B’ :

-  On utilise la relation du grandissement de l’image :

-  

-  Schéma final :

-  L’image formée à travers la lentille ne peut pas être observée sur un écran.

-  Ce sont les prolongements des rayons lumineux qui se coupent en B’

-  L’image est virtuelle.

-  Elle ne se forme pas sur un écran mais elle peut être vue par l’œil à travers le système optique.

-  Il faut placer l’œil sur le chemin des rayons lumineux qui émergent du système optique.

IV- Applications.

1)- TP : Relations pour une lentille mince convergente.

Les lentilles convergentes

2)- L’appareil photographique et l’œil.

a)-  L’appareil photographique.

Vision et images

-  C’est un instrument d’optique qui permet de former l’image d’un objet.

-  Schéma :

-  Le modèle de l’appareil photographique.

-  En simplifiant, on peut résumer le mécanisme de l’appareil photographique :

-  Le diaphragme permet de régler l’énergie lumineuse qui pénètre dans l’appareil photographique

-  L’objectif peut être assimilé à une lentille convergente L à laquelle on appliquera les lois des lentilles minces.

-  Quand on règle l’appareil pour obtenir une image nette, la vergence de cette lentille varie.

-  Pour voir nettement, un objet, il faut que l’image se forme sur le film ou le capteur situé derrière la lentille L.

-  Schéma simplifié :

b)-  L’œil.

-  L’œil peut être assimilé à une sphère, de 2,3 cm de diamètre, limitée par une membrane très résistante et sombre : la sclérotique.

-  Schéma :

►  Comme dans le cas des instruments d’optique, on retrouve :

-  Un ensemble optique assurant la formation des images.

-  Les rayons lumineux traversent une succession de milieux transparents d’indices de réfraction différents :

-  La cornée (n = 1,376),

-  L’humeur aqueuse (n = 1,337), le cristallin (n = 1,437 : il a la forme d’une lentille biconvexe), l’humeur vitrée (n = 1,337).

-  La pupille, ouverture circulaire (dont le diamètre varie de 2 mm à 8 mm), joue le rôle de diaphragme.

-  Elle règle le flux lumineux.

-  La rétine, membrane tapissée de cellules photosensibles (cônes et bâtonnets), joue le rôle de récepteur de lumière.

►  Modèle de l’œil.

-  En simplifiant, on peut résumer le mécanisme de vision de l’œil ainsi :

-  La pupille joue le rôle de diaphragme

-  L’ensemble {cristallin + cornée} peut être assimilé à une lentille convergente L à laquelle on appliquera les lois des lentilles minces.

-  Quand on « accommode », la vergence de cette lentille augmente.

-  Pour voir nettement, un objet, il faut que l’image se forme sur la rétine située 17 mm derrière la lentille L.

-  Faire un schéma du dispositif expérimental permettant de modéliser l’œil.

-  Indiquer les dimensions.

-  Schéma :

-  Remarque :

-  Au cours de la séance de travaux pratiques, on modélise un œil normal au repos à l’aide d’un tube cylindrique, de longueur ℓ₁, aux extrémités duquel sont fixés une lentille convergente et un écran (verre dépoli ou papier translucide).

-  Pour fabriquer l’œil modélisé normal, on place l’écran (la rétine) à 17 cm de la lentille.

3)- QCM.

Réalisé avec le logiciel Questy

Pour s'auto-évaluer

Les relations de conjugaison et de grandissement

Le lien entre la position de l'objet et les caractéristiques de l'image

Sous forme de tableau

4)- Exercices :