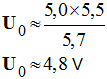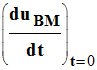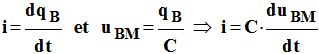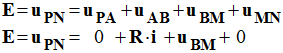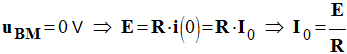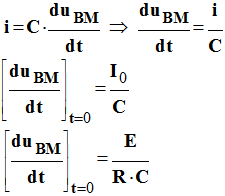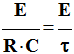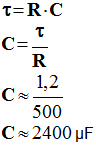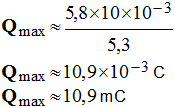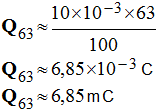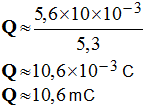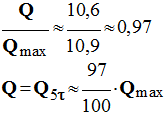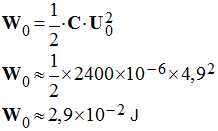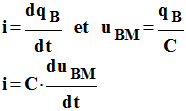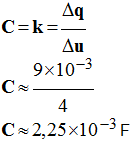1)- But.

Observer l’évolution de la tension aux bornes d’un condensateur chargé par un générateur de tension  en série avec une résistance R.

Évaluer expérimentalement la constante de temps τ du circuit R.C.

Observer l’évolution de l’intensité i du courant lors de la charge et de la décharge du condensateur.

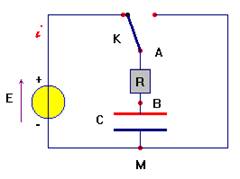
2)- Montage.                              

Indiquer les branchements nécessaires à la visualisation de la variation de la tension aux bornes du condensateur en fonction du temps.

- Branchements :

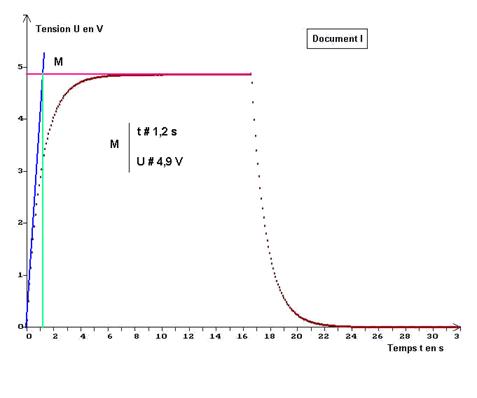
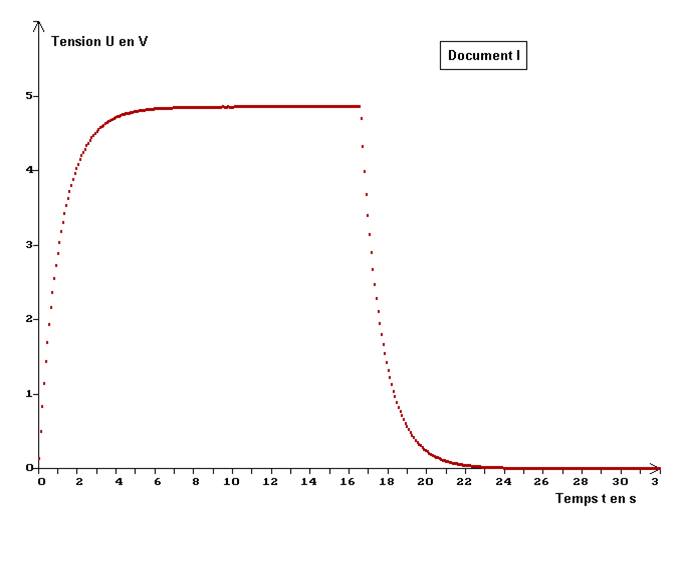
1)- Étude de u_BM = f (t).

a)- Quel est le document qui représente les variations de la tension u_BM enfonction du temps ?

-  document qui représente les variations de la tension u_BM en fonction du temps : Document I.

b)- Nommer les deux phases de la charge ou de la décharge du condensateur.

-  les deux phases de la charge ou de la décharge du condensateur :

-  Régime transitoire et régime permanent.

c)- Quelle est l’ordonnée de l’asymptote horizontale à la courbe représentant la charge du condensateur ?

-  ordonnée de l’asymptote horizontale à la courbe représentant la charge du condensateur :

-  

d)- Interpréter le résultat et en déduire la valeur de la tension aux bornes du condensateur lorsqu’il est chargé.

-  Interprétation du résultat : U₀ représente la valeur de la tension, aux bornes du condensateur  lorsqu’il est chargé.

e)- Déterminer l’expression littérale de  . Tracer la tangente à l’origine à la courbe.

Donner les coordonnées du point M, point d’intersection de la tangente à l’origine à la courbe et de l’asymptote horizontale à la courbe.

En déduire la valeur de la constante de temps t du circuit R.C.

-  Expression littérale de  :

-  On connaît : 

- 

-  additivité des tensions :

-  

-   Au temps t = 0 s :  

- 

-  Or

- 

-  tangente à l’origine à la courbe.

-  valeur de la constante de temps :

-  τ = R.C ≈ 1,2 s  car  le rapport  donne le coefficient directeur de la tangente à l’origine de la courbe : u_BM = f (t).

f)-  Calculer la valeur de la capacité C du condensateur sachant que la résistance

 R = 500 Ω. La comparer avec celle donnée par le constructeur (C = 2200 μF).

-  Valeur de la capacité C du condensateur.

-  

-  Précision sur la mesure :

-  

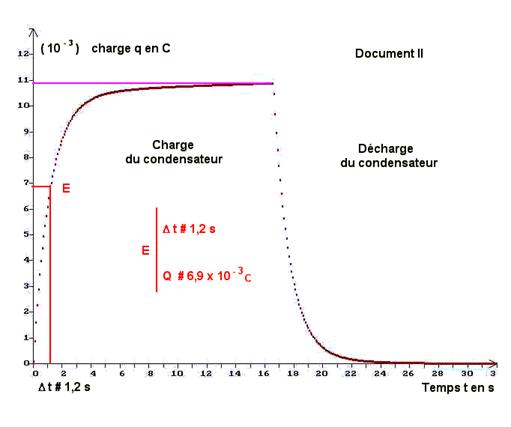
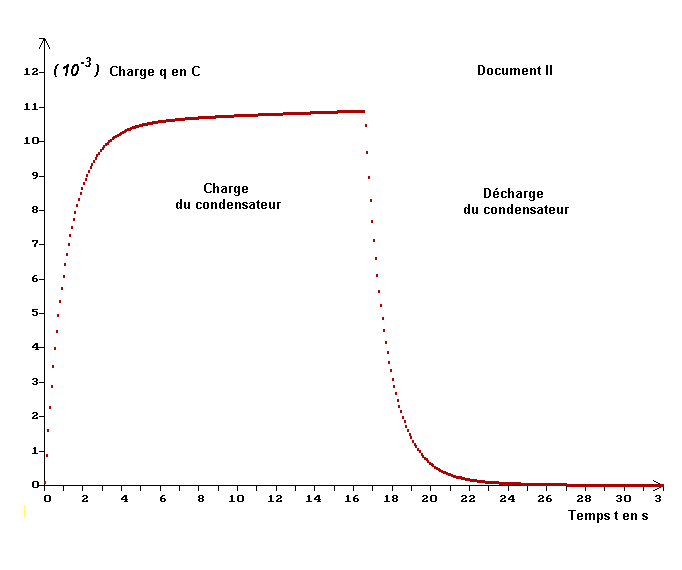
-  cette méthode de détermination de τ puis de C est peu précise (imprécision sur le tracé de la tangente à l’origine).

2)- Étude de q_B = f (t).

a)- Quel est le document qui représente les variations de la charge q_B en fonction du temps ?

-  document qui représente les variations de la charge q_B en fonction du temps : Document II.

b)- Déterminer la valeur de la charge maximale Q_max emmagasinée par le condensateur.

-  valeur de la charge maximale Q_max emmagasinée par le condensateur :

-  

c)-   Calculer la durée au bout de laquelle le condensateur est chargé à 63 % de sa valeur maximale.

Comparer cette durée à la constante de temps t.

-  durée au bout de laquelle le condensateur est chargé à 63 % de sa valeur maximale :

-    

-  Graphiquement, on trouve :  Δt ≈ 1,2 s.

-  On remarque que Δt ≈ τ ≈ 1,2 s

d)- Déterminer la charge du condensateur au bout de la durée Δt = 5 τ.

-  charge Q du condensateur au bout de la durée Δt = 5 τ.

-  Δt = 5 τ ≈ 6,0 s

-  

e)- Exprimer Q en fonction de la charge maximale Q_max. Conclusion.

-  

-  On peut considérer qu’au bout de 5 τ, le condensateur est pratiquement chargé.

f)-  Calculer l’énergie W₀ emmagasinée par le condensateur lorsqu’il est chargé.

-  énergie W₀ emmagasinée par le condensateur lorsqu’il est chargé :

- 

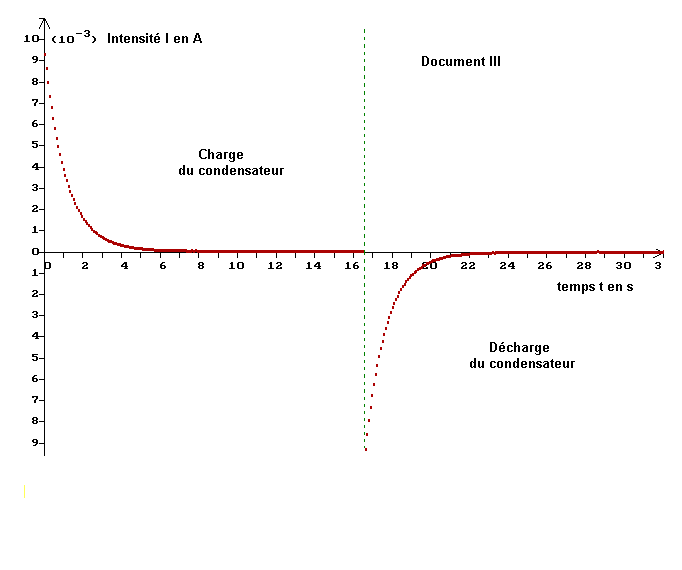
3)- Étude de i = h (t).

a)- Quel est le document représentant les variations de l’intensité du courant dans le circuit en fonction du temps ?

-   Intensité du courant dans le circuit en fonction du temps : Document III.

b)- Comment varie la valeur de l’intensité du courant lors de la charge du condensateur ?

Quelle est la valeur de l’intensité dans le circuit lorsque le condensateur est chargé ?

-  L’intensité du courant diminue au cours de la charge du condensateur.

-  Lorsque le condensateur est chargé, l’intensité dans le circuit est nulle.

c)-   Exprimer en fonction de la charge q_B de l’armature du condensateur reliée aupoint B l’intensité i dans le circuit et la tension u_BM aux bornes du condensateur.

En déduire l’expression de i en fonction de u_BM.

-  Relation :

- 

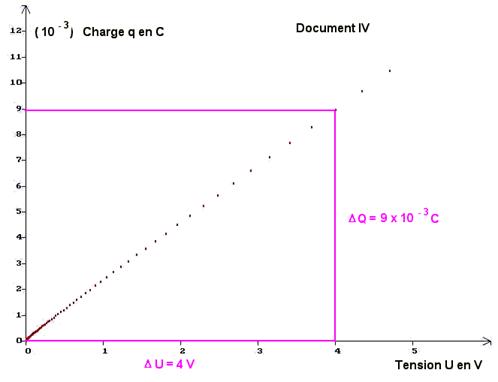
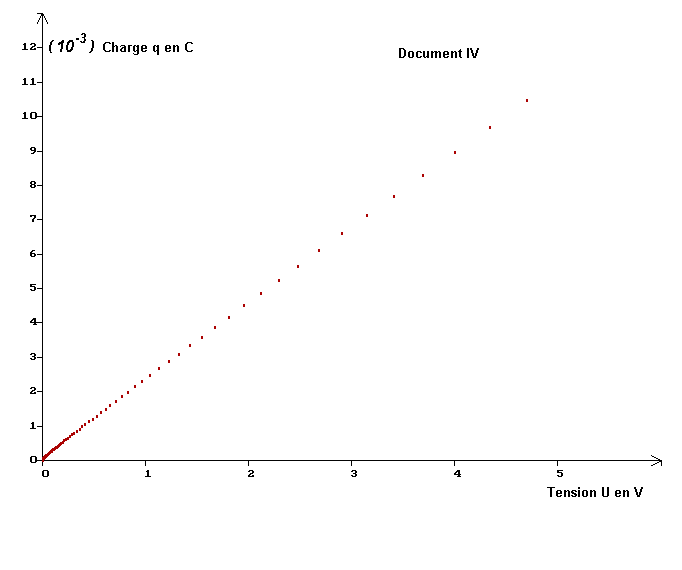
4)- Étude de q_B = f (u_BM).

a)- Quel est le document représentant les variations de q_B en fonction de u_BM ?

-  variations de q_B en fonction de u_BM : Document IV.

b)- En déduire une relation simple entre ces deux grandeurs. Que représente le coefficient directeur de la droite obtenue ?

Calculer sa valeur. Quelle est son unité ? Que représente cette grandeur ?

-  Relation simple entre ces deux grandeurs :

-  La courbe obtenue est une droite qui passe pratiquement par l’origine.

-  La charge q du condensateur est proportionnelle à la tension entre ses bornes :

-  u_BM : q = k . u_BM

-  le coefficient directeur de la droite obtenue représente le coefficient de proportionnalité k.

-  Unité de k :  

-  C / V. c’est le farad F.

-  k représente la valeur de la capacité du condensateur :

-  

-  

-   Cette méthode de détermination de C est plus précise.