|
TP Physique N° 08 |
Principe de l'Inertie. Enoncé. |
|
|
Programme 2010 : Physique et Chimie Programme 2020 : Physique et Chimie |
|
|
Matériel : mobile autoporteur, deux stylets, table plane et horizontale.
1)- Dispositif expérimental.
- Il est constitué d’une table horizontale et d’un mobile autoporteur. Il est équipé d’une soufflerie afin d’éliminer (pratiquement) les forces de frottement.
- On peut considérer que les frottements sont négligeables.
- Le mobile est muni de deux stylets : un au centre G et l’autre à sa périphérie A.
- À intervalles de temps égaux ( τ = 20 ms), les stylets indiquent leur position sur la feuille en la brûlant ponctuellement.
2)- Expérience.
- Le mobile est lancé sur la table horizontale avec un effet de rotation.
|
|
|
|
3)- Étude du système.
- Système : S = {mobile autoporteur}
- Référentiel : la table horizontale. Comme elle est liée à la Terre, on utilise un référentiel terrestre.
4)- Exploitation de l’enregistrement.
Déterminer la
vitesse moyenne du point A, puis du point G entre les instants
t
1
et t
20.
Déterminer leur
vitesse instantanée aux dates
t
11
et t
16.
|
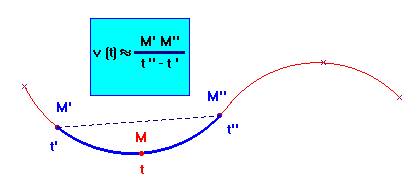
ʘ - On va considérer que pendant un intervalle de temps très court, la vitesse ne varie pratiquement pas, qu'elle reste pratiquement constante. - On
peut en conséquence utiliser la relation précédente. La vitesse instantanée v(t) d’un point mobile, à la date t, est pratiquement égale à sa vitesse moyenne calculée pendant un intervalle de temps très court encadrant l’instant t considéré. |
-
Écriture simplifiée : vitesse du point mobile à l’instant
t3 :
-
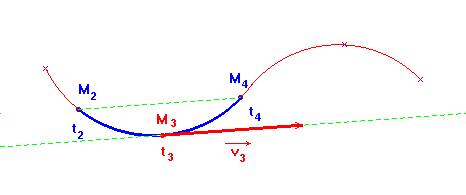
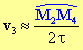
Que peut-on dire de la
vitesse instantanée du point
G ?
pour le point
G
comparer la
vitesse moyenne et la vitesse instantanée. Conclusion.
Quelle est la nature de la
trajectoire du point
A ?
Du point G ?
5)- Conclusion.
Quelle est la nature du
mouvement du point
A ?
Du point B ?
II-
Le référentiel barycentrique.
1)- Trajectoire du point A.
- Le point G est le barycentre du système.
- On va étudier le mouvement du point A dans le référentiel barycentrique.
- On va étudier le mouvement du point A par rapport au point G.
- Référentiel : le point G.
Méthode : pour cela, il faut pouvoir immobiliser le point
G.
sur une feuille de papier calque, placer au centre un point
G
et représenter un repère orthonormé ayant
G
pour origine.
- Faire coïncider le point G de la feuille de papier calque avec le point G 0 de l’enregistrement et noter la position du point A0 sur la feuille de papier calque.
- Faire glisser la feuille de papier calque parallèlement à la feuille afin de faire coïncider G et G 1 et noter la position du point A 1 et ainsi de suite.
|
|
|
|
2)- Exploitation du tracé.
Quelle est la nature de la
trajectoire du point
A ?
Calculer la vitesse
instantanée en deux points.
Que peut-on dire de la valeur
de la vitesse instantanée ?
En déduire la nature du
mouvement.
La vitesse du point A
est-elle la même dans le référentiel : table horizontale ?
Conclusion.
III-
Le principe de l’inertie.
1)- Bilan des forces qui s’exercent sur le système.
- On travaille dans le référentiel : table horizontale (référentiel terrestre) avec un système S = {mobile autoporteur} qui est soit immobile, soit en mouvement.
-
Le mobile autoporteur est soumis à son poids : 
force
verticale orientée du haut vers le bas.
-
À l’action de
la soufflerie : 
force verticale orientée du bas vers le haut.
- Lorsque le mobile se déplace sur un plan horizontal ou lorsqu’il est immobile, P = R.
-
et
ont même direction, même valeur et sont de sens contraires.
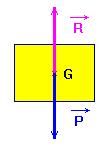
Construire
( et ayant même valeur,
on les représentera par des segments fléchés de même longueur).
- Remarque : lorsque la somme vectorielle des forces qui s’exercent sur un système est égale au vecteur nul, on dit que ces forces se compensent.
2)- Principe de l’inertie.
- Dans un référentiel terrestre, lorsque les forces appliquées à un système se compensent, alors le centre d’inertie G du système est soit immobile, soit animé d’un mouvement rectiligne uniforme.
3)- Remarque.
- Si l’on supprime la soufflerie, il y aura des forces de frottement en plus du poids et de la réaction de la table.
-
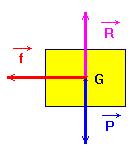
les forces ne se compensent pas.
G n’est pas animé
d’un mouvement rectiligne uniforme.
- Sa vitesse diminue au cours du temps jusqu’à ce que le mobile s’arrête.
|
|
Mouvement d’une bille dans un liquide.
On lâche la bille sans vitesse initiale dans l’huile contenue dans une grande éprouvette graduée de 500 mL. La chute de la bille a été enregistrée par chronophotographie. La caméra prend 50 images par seconde. 1)- Dans quel référentiel étudie-t-on le mouvement de la bille ? 2)- Décrire le mouvement de la bille dans ce référentiel. 3)- Déterminer la valeur de la vitesse moyenne vmoy de la bille entre les deux positions extrêmes. 4)- Déterminer la valeur de la vitesse instantanée aux temps t8 et temps t14. 5)- À partir de quelle position peut-on dire que les forces qui agissent sur la bille ont des effets qui se compensent ? On appelle vitesse limite, la vitesse de la bille à partir de cette position. 6)- Déterminer la valeur vlim de cette vitesse limite par deux méthodes.
|
