|
Phys. N° 02 |
Mouvements d’un Solide : exercices |
|
Programme 2011 :
Physique et
Chimie Programme 2020 :
Physique et
chimie
Pour aller plus loin :
|
Mots clés : Mouvement ; mouvement de translation ; mouvement de rotation ; vitesse ; vecteur vitesse ; centre d'inertie d'un solide ; ... |
|
|
Applications :
|
Exploiter
une chronophotographie :
Le document ci-contre est la chronophotographie d’une roue de bicyclette dont le cadre est maintenu immobile. On a collé une pastille blanche sur un rayon. L’intervalle de temps entre deux prises de vue consécutives est égal à 40 ms. 1. Caractériser le mouvement de la roue. 2. Déterminer la vitesse angulaire ω de la roue. 3. Calculer la valeur v de la vitesse d’un point situé à sa périphérie. 4. Déterminer la période T de rotation de la roue.4. Donnée : diamètre de la roue D = 50 cm |
Correction :
|
1. Caractéristiques du mouvement
de
- La roue (mobile) est animée d’un mouvement de rotation autour d’un axe fixe par rapport à la fourche (Référentiel).
-
L’axe de rotation de la roue est
perpendiculaire au plan de la roue et
passe par le centre de la roue. - Le mouvement de la roue est
uniforme car le disque blanc parcourt des arcs égaux pendant des durées
égales (
τ = 40 ms) 2. Vitesse angulaire de la
roue : - Pour faire un tour, la roue met la durée suivante : - Δt = 10 τ
-
Δt ≈
3. Valeur de la vitesse
v
d’un point situé à la périphérie : - Relation :
4. Période de rotation de
la roue. - La roue effectue un mouvement périodique : - Un phénomène périodique est
un phénomène qui se reproduit de manière identique au bout d’une
durée appelée période, notée
T. - Ici la période est la durée
pour effectuer un tour :
T
= 0,40 s - On peut en déduire la fréquence
du mouvement de la roue :
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Déterminer une vitesse angulaire : Le tambour d’une machine à laver le linge est un cylindre de 46 cm de diamètre. Au moment de l’essorage, il tourne autour de son axe à 800 tr / min. 1. Calculer sa vitesse angulaire ω de rotation. 2. Calculer la vitesse v d’un point de la périphérie du tambour. |
Correction :
|
1. Vitesse angulaire du
tambour de
2. Vitesse d’un point de la périphérie du tambour :
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Les
Satellites d’observation de
1- La
période de rotation de
- Calculer la valeur de la vitesse d’un point situé : - Sur l’équateur ; - À une latitude de 60 ° Nord ; - À une latitude de 60 ° Sud.
2- Le
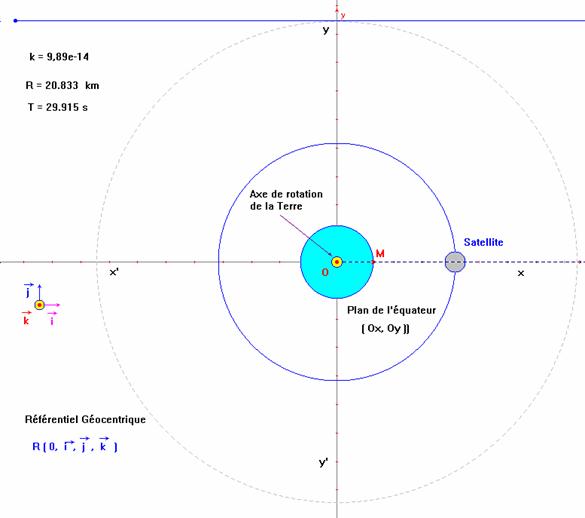
satellite géostationnaire Météosat, assimilable à un point matériel,
est situé à la distance de 42200 km du centre de
a. Décrire son mouvement dans le référentiel géocentrique. b. Déterminer sa vitesse angulaire ω dans le référentiel géocentrique. c. Calculer sa vitesse dans le référentiel géocentrique.
|
Correction :
Voir
animation géostationnaire

|
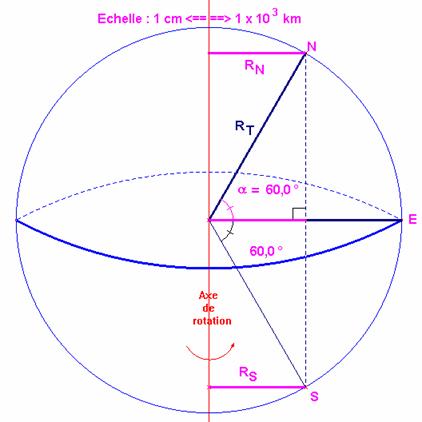
1. Vitesse d’un point : - Schéma des différentes situations :
- Vitesse d’un point situé sur l’équateur E : - - Vitesse d’un point situé dans l’hémisphère Nord N : - - Vitesse d’un point situé dans l’hémisphère Nord N : - Idem : 2. Mouvement de Météosat : a) Caractéristique du mouvement de Météosat : - Dans le référentiel Géocentrique, le satellite Météosat
décrit une trajectoire circulaire de rayon
R =
Le temps mis pour faire un tour T = 86164 s (période du mouvement). Le satellite est animé d’un mouvement circulaire uniforme. b) Vitesse angulaire du satellite dans le référentiel géocentrique :
c) Vitesse du satellite dans le référentiel géocentrique :
3. Période de rotation du satellite Spot : - C’est le temps mis par le satellite pour faire un tour. - On utilise la formule trouvée précédemment : - - La
période TS
< T
= 86164 s. Le satellite est en mouvement par rapport à - Ce n’est pas un satellite géostationnaire. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||